Пример моделирования РТК

Планировка РТК приведена на рис. 244. Промышленный робот ПР загружает и разгружает два станка ТО1 и ТО2. В процессе загрузки-разгрузки робот взаимодействует с двумя накопителями Н1 и Н2, предназначенных для заготовок и обработанных деталей.

Промышленный робот ПР (при условии его свободного исходного состояния и наличия заготовки во входном накопителе Н1)берет заготовку из накопителя и устанавливает ее в патрон станка ТО1 (траектория 1). После зажатия заготовки кулачковым патроном станкапромышленный робот перемещает руку к патрону станка ТО2 (траектория 2) и осуществляет цикл его разгрузки. Он удаляет со станка обработанную деталь и укладывает её ее в накопитель Н2(траектория 3). После окончания обработки заготовки на станке ТО1, робот перемещает руку в его рабочую зону (траектория 4), вынимает деталь из патрона и перемещает её на станок ТО2 (траектория 5). После загрузки этого станка робот переходит в исходное состояние (траектория 6) и цикл работы РТК заканчивается.

Выделим следующие позиции и переходы для сети Петри:

Р0 – во входном накопителе РТК есть запас заготовок;

Р1 – ПРзагружает станок ТО1;

Р2 – ПР свободен и готов к загрузке первого станка;

РЗ – обработка заготовки на станке ТО1;

Р4 – станок ТО1 свободен и готов к работе;

Р5 – ПР свободен и готов разгрузить станок ТО2;

Р6 – ПР в состоянии транспортирования детали с ТО1 на ТО2;

Р7 – обработка заготовки на станке ТО2;

Р8 – станок ТО2 свободен и готов к работе;

Р9 – ПР в состоянии разгрузки станка ТО2;

Р10 –ПР свободен и готов к разгрузке станка ТО1;

Р11 – обработанная деталь в накопителе Н2;

t1 – заготовка взята из входного накопителя H1;

t2 – заготовки загружена на станок ТО1;

t3 – станок ТО1 разгружен;

t4 – заготовка загружена на станок ТО2;

t5 – станок ТО2 разгружен;

t6 – обработанная деталь помещена в выходной накопитель Н2.

Сеть Петри, моделирующая рабочий цикл РТК, представлена на рис. 245. Для построения графа достижимости, описывающего возможные варианты функционирования сети Петри, необходимо определить начальную маркировку сети

Граф достижимости можно строить, используя непосредственное отслеживание движения маркеров по сети Петри, или по результатам аналитических преобразований в матричной форме с вычислением составной матрицы изменений D

.

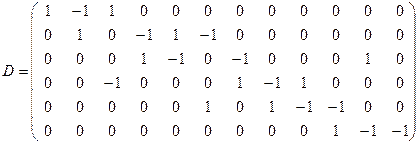Граф достижимости мы не приводим, укажем только, что, последовательно проходя пять маркировок, сеть Петри приходит в исходное состояние и начинает новый цикл. Таким образом, в сети отсутствуют тупиковые маркировки, следовательно, РТК работоспособен.