Пример моделирования ГПМ для обработки валов

Рассмотрим ГПМ для обработки валов, который включает два станка с ЧПУ токарной группы и портальный промышленный робот, обслуживающий эти станки. Предположим, что при обслуживании первого станка робот занят всё время, пока станок работает. Для второго станка робот выполняет только его загрузку и разгрузку. Возможные состояния ГПМ выделим укрупнено: Р₁ – наличие заготовки; Р₂ – свободен первый станок 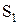; Р₃ – станок 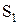работает; Р₄ – свободен промышленный робот ПР; Р₅ – станок 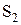работает; Р₆ – станок 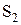свободен; Р₇ – наличие готовой детали.

Таким образом, множество состояний ГПМ Р{Р₁, Р₂, Р₃, Р₄, Р₅, Р₆, Р₇}. Учтем следующие события: 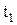– загрузку станка 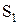; 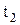– загрузку станка 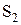; 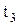а – разгрузку станка 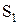; 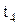– разгрузку станка 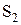. Следовательно, множество событий (переходов) .

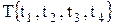На основе анализа связи состояний и событий функции входных и выходных инциденций для модуля можно представить в следующем виде:

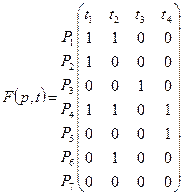
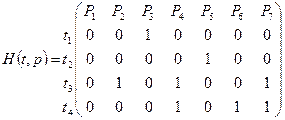
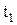Для начальной маркировки примем m₀(Р) = (9, 1, 0, 1, 0, 1, 0). Изображение сети Петри для моделируемого ГПМ будет иметь вид (рис. 242). Из начальной маркировки сети возможны переходы и 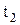. Построим фрагмент графа достижимости рассматриваемой сети (рис. 243). Если произойдёт переход t₁, то начнёт работать станок S₁, а промышленный робот будет занят ожиданием конца работы станка. В этом состоянии возможен только переход t₃.

Если же в начальный момент времени совершится переход t₂ и начнёт работать второй станок, то освободившийся после загрузки второго станка промышленный робот может приступить к загрузке первого станка, т.е. становится возможным переход t₁. Все эти переходы и изменения состояний ГПМ хорошо просматриваются на графе достижимости сети Петри.

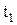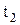На основе анализа графа достижимости выбирается требуемый цикл работы ГПМ. Если одновременно в сети возможны несколько событий, то следует для них установить приоритеты. Например, в рассматриваемом случае, если одновременно возможны события и (загрузка станков 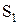и 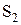), то установка более высокого приоритета события 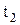позволит уменьшить простой станка 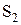, т. к. при первоочередной загрузке станка 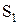робот будет занят до окончания работы и разгрузки 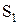, а станок 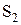все это время будет простаивать.

Основным недостатком графа достижимости является то, что он не связан со временем функционирования моделируемой системы и не позволяет оценить временные затраты как на отдельные элементы рабочего цикла, так и на рабочий цикл в целом. Использование расширения сети Петри с задержкой маркера в позиции позволяет устранить этот недостаток и получить временные характеристики процесса в моделируемой системе.