Моделирование производственной системы конечным автоматом
Производственная система в целом, её отдельные технологические модули и технологическое оборудование характеризуются набором дискретных состояний и сигналов, т. е. такие системы являются дискретными. В процессе функционирования дискретной системы в ней происходит последовательная смена состояний в соответствии с рабочим циклом. Переход из состояния в состояние инициируется дискретными (логическими) сигналами управления, имеющими смысл: включить – выключить. При описании и исследовании дискретных систем используются соответствующие методы: дискретная оптимизация, ориентированные графы, теория конечных автоматов, сети Петри и др.
Для формализованного описания дискретных систем получил распространение метод конечного автомата. Метод конечного автомата применим для описания дискретных объектов, обладающих следующими свойствами:
· объект управления в каждый момент времени находится в одном из множества возможных для него дискретных состояний;
· переход объекта из состояния в состояние инициируется подачей на его входы логических управляющих сигналов, которые образуют множество входных сигналов объекта;
· текущее состояние объекта характеризуется дискретными (логическими) выходными сигналами, которые формируются датчиками, установленными на объекте и зависят от текущего состояния объекта и его входных сигналов;
· взаимосвязь между входными, выходными сигналами и состояниями объекта описывается логическими выражениями;
· при функционировании объекта происходит смена его состояний в определенной последовательности.
Обобщенным формализованным описанием дискретного объекта является конечный автомат. Конечный автомат – это математическая модель, включающая следующие компоненты описания:
A{X, Y, S, f, 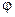 },
},
где Х(X1, X2, X3...) – множество входных логических сигналов;
Y(Y1, Y2, Y3...) – множество выходных логических сигналов;
S(S1, S2, S3...) – множество внутренних состояний автомата;
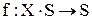 – функция переходов, определяющая новое состояние объекта в зависимости от его предыдущего состояния и входных сигналов;
– функция переходов, определяющая новое состояние объекта в зависимости от его предыдущего состояния и входных сигналов;
 – функция выходов автомата, определяющая новое значение выходных сигналов в зависимости от текущего состояния автомата и входных сигналов.
– функция выходов автомата, определяющая новое значение выходных сигналов в зависимости от текущего состояния автомата и входных сигналов.
 Конечный автомат может быть представлен черным ящиком, на входы которого поступают n логических сигналов X, который может находиться в одном из Si (i = 1,…,m) состояний и на выходе которого присутствуют k логических сигналов Y (рис. 236).
Конечный автомат может быть представлен черным ящиком, на входы которого поступают n логических сигналов X, который может находиться в одном из Si (i = 1,…,m) состояний и на выходе которого присутствуют k логических сигналов Y (рис. 236).
Функцию переходов и функцию выходов конечного автомата можно представить в виде таблиц, пример которых приведен ниже. В строках таблиц указываются входные сигналы, а в столбцах – возможные состояния автомата. Затем в ячейках таблицы переходов записываются новые значения состояний, соответствующие определенному исходному состоянию и входному сигналу, или значения выходных сигналов в тех же условиях.
| F | S | |||
| X | S1 | S2 | … | Sm |
| X1 | - | S4 | … | S7 |
| X2 | S7 | - | … | S2 |
| … | … | … | … | … |
| Xn | S4 | S3 | … | S4 |
| j | S | |||
| X | S1 | S2 | … | Sm |
| X1 | Y1 | Y5 | … | Y2 |
| X2 | Y2 | Y3 | … | Y4 |
| … | … | … | … | … |
| Xn | Y1 | Y2 | … | Yk |
В процессе функционирования объекта описания изменяются состояния последнего, его входные и выходные сигналы. Этот процесс порождает функционирование конечного автомата. Функционирование конечного автомата заключается в смене его состояний и выходных сигналов при смене входных сигналов.
Для графического представления функционирующего автомата используется направленный граф
 ,
,
где V(V1, V2, V3...) – множество вершин графа, отображающих состояния автомата;
U(U1, U2, U3...) – множество звеньев, соединяющих вершины графа и отображающих функцию переходов и функцию выходов автомата;
 – функция инцидентности, описывающая связи между вершинами графа.
– функция инцидентности, описывающая связи между вершинами графа.
Функция инцидентности разбивает все множество звеньев на три подмножества: подмножество ребер 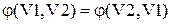 , подмножество дуг
, подмножество дуг  подмножество петель
подмножество петель 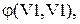 .
.
Ребра графа (связь вершин V1 и V2) определяют ненаправленные связи, дуги – направленные, а петли (связь вершины 1 с собой) имеют в качестве начала и конца одну и ту же вершину. Если граф не содержит ребер, то он называется ориентированным
Состояния конечного автомата отображаются вершинами графа. Дуги и петли графа отображают изменения входных и выходных сигналов конечного автомата. Вершины графа изображаются в виде окружностей, в которых записывается символическое обозначение соответствующего состояния. Входные и выходные сигналы приписываются звеньям графа. При этом входной сигнал записывается непосредственно над линией, изображающей звено графа, а выходной – в скобках после входного сигнала. Указываются только те сигналы, значение которых изменяется при конкретном переходе между вершинами.
Моделирование дискретного объекта с помощью конечного автомата осуществляется в определенной последовательности:
1. На основе анализа схемно-технических решений объекта и описания его работы выделяются и описываются все возможные дискретные состояния объекта. Формируется множество конечных состояний конечного автомата.
2. Описываются все входные управляющие сигналы объекта, и формируется множество входных логических сигналов конечного автомата.
3. Описываются все выходные логические сигналы объекта, и формируется множество выходных сигналов конечного автомата.
4. Формулируются логические выражения для описания связей между состояниями объекта, его входными и выходными сигналами. Заполняются таблицы, описывающие функции переходов и выходов конечного автомата.
5. Составляется граф функционирования конечного автомата.
Граф функционирования конечного автомата позволяет выявить возникающие при функционировании объекта противоречия, недостаточность или избыточность его сигналов управления и информационных сигналов. На основе графа функционирования разрабатывается алгоритм управления объектом.
Рассмотрим в качестве примера моделирование ГПМ, который характеризуется набором дискретных информационных сигналов, логическими сигналами управления и дискретными состояниями. Модель ГПМ можно представить в виде конечного автомата, для которого составляется граф функционирования. Вершинами графа будут состояния ГПМ, а дугами – условия перехода из состояния в состояние (значения сигналов).

На рис. 237, а приведен конечный автомат для описания системы управления ГПМ: X – логические входные сигналы, поступающие от датчиков ГПМ и локальных устройств управления, Y – управляющие команды и выводимые сообщения, S – состояния ГПМ. Функции переходов и функции выходов конечного автомата отображены на графе функционирования (рис. 237, б).
Дуги графа отображают условия перехода ГПМ из одного состояния в другое и изменяющиеся при переходе выходные сигналы конечного автомата. Граф позволяет наглядно отображать функционирование моделируемого объекта и служит основой для формирования алгоритма управления.
Направленные графы имеют ограниченные возможности отображения свойств дискретных процессов. Более широкими возможностями моделирования дискретных процессов обладают сети Петри.
Дата добавления: 2015-07-30; просмотров: 2117;
