Принцип взаимности. Линейные электрические цепи обладают принципом взаимности
Линейные электрические цепи обладают принципом взаимности. Этот принцип можно сформулировать применительно к источнику ЭДС или тока. Сформулируем этот принцип применительно к источнику ЭДС.
На рис. 36 изображены две схемы электрической цепи, в каждой из которых выделены по две ветви q и p. В каждой схеме имеется только один источник ЭДС. На рис. 36, а источник ЭДС расположен в ветви q, а на рис. 36, б аналогичный источник находится в ветви p. Оставшаяся часть схемы может иметь произвольную структуру, важно, что эта структура для обоих рисунков одинакова.
а) 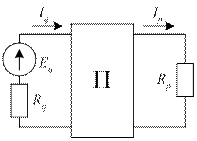 б)
б) 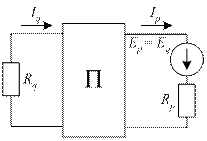
Рис. 36. Схемы с источником ЭДС в ветви q (а) и ветви p (б)
Принцип взаимности формулируется следующим образом.
В любой сколь угодно сложной линейной электрической цепи ток в ветви p, созданный ЭДС Eq, находящейся в ветви q (рис. 36 а) будет равен току Iq в ветви q, созданному ЭДС Ep = Eq, находящейся в p-й ветви (рис. 36 б).
Для доказательства принципа взаимности воспользуемся методом контурных токов, и выберем независимые контура так, чтобы ветви q и p являлись внешними ветви (хордами). Тогда токи этих ветвей будут совпадать с контурными токами. С учетом этого из формулы (10) для схемы рис. 36 а получаем:
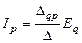 .
.
Аналогичным образом для схемы рис. 36 б имеем:
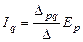 .
.
В этих двух выраженияхEp = Eq, Δpq = Δqp. Следовательно, Ip = Iq и принцип взаимности доказан.
Из последних двух соотношений имеем также:
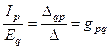 и
и 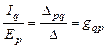 .
.
Проводимость gpq = gqpназывается взаимной или передаточной проводимостью ветвей q и p. Взаимная проводимость двух ветвей определяется как отношение тока одной ветви к ЭДС другой ветви.
Если в последних двух соотношениях рассматривать ток и ЭДС применительно к одной ветви q или p, то получим:
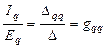 или
или 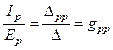 .
.
Проводимости gqq и gpp называются входными проводимостями ветвей q и p. Входная проводимость ветви представляет собой отношение тока ветви, содержащей единственный в схеме источник ЭДС, к величине ЭДС.
Величина, обратная входной проводимости, называется входным сопротивлением ветви:
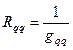 или
или 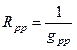 .
.
Аналогичным образом взаимное сопротивление двух ветвей определится как
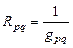 или
или 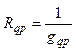 .
.
Дата добавления: 2015-07-24; просмотров: 3688;
