Метод узловых потенциалов
В методе узловых потенциалов сначала определяются потенциалы всех узлов схемы по отношению к одному из узлов, потенциал которого условно принимается равным нулю. Далее с помощью закона Ома для участка цепи с источником ЭДС рассчитываются токи в ветвях схемы.
Покажем возможность такого подхода. Рассмотрим схему рис. 27.
Схема содержит семь ветвей и четыре узла. Параметры схемы известны. Требуется определить токи ветвей.
Заземлим один из узлов схемы, например, узел c и примем его потенциал равным нулю (φc = 0). Для определения потенциалов оставшихся (n – 1) узлов необходимо составить систему из (n – 1) уравнения относительно неизвестных потенциалов.
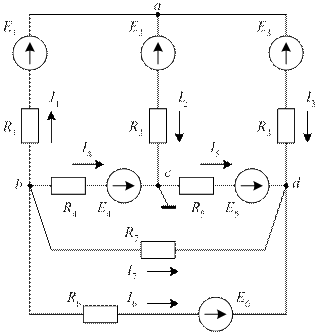
Рис. 27. К методу узловых потенциалов
Для вывода этой системы зададимся положительными направлениями токов в ветвях и для узлов a, b, d (рис. 27) составим уравнения по первому закону Кирхгофа:
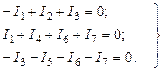
Полученная система из трех уравнений содержит семь неизвестных токов и решения не имеет. Необходимо свести ее к системе из трех уравнений с тремя неизвестными. В качестве таких неизвестных целесообразно представить потенциалы узлов a, b, d.Выразим токи ветвей через потенциалы узлов, ЭДС источников и проводимости ветвей:
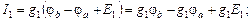
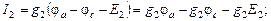
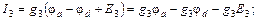
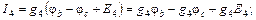
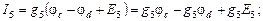
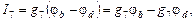
где потенциалы φa, φb, φd пока неизвестны, потенциал φc = 0, а проводимости ветвей есть величины обратные сопротивлениям ветвей
g1 = 1/R1, g2 = 1/R2, g3 = 1/R3, g4 = 1/R4, g5 = 1/R5, g6 = 1/R6, g7 = 1/R7.
Подставив выражения для токов ветвей в исходную систему уравнений, сгруппировав в левой части члены, содержащие неизвестные потенциалы φa, φb, φd, и перенеся в правую часть члены, не содержащие неизвестных величин, получим следующую систему уравнений
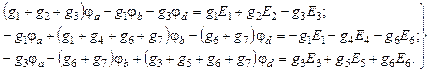
Эту систему уравнений можно записать иначе в общем виде, справедливом для любой схемы с четырьмя узлами
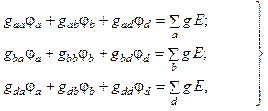
где gaa, gbb, gdd – собственные проводимости узлов a, b, d (суммы проводимостей ветвей, входящих в каждый из этих узлов); gab=gba, gad=gda, gbd=gdb – смежные проводимости узлов a, b, d (суммы проводимостей ветвей, соединяющих пары узлов, взятые со знаком минус).
В правых частях уравнений рассматриваемой системы берутся алгебраические суммы произведений gE для ветвей, входящих соответственно в узлы a, b, d. Причем члены этих сумм берутся со знаком плюс, если стрелка источника ЭДС направлена к соответствующему узлу, и со знаком минус, если стрелка направлена от узла.
Из решения рассматриваемой системы уравнений определяются потенциалы узлов a, b, d, а по ним с помощью закона Ома для участка цепи с источником ЭДС – токи ветвей.
Рассматриваемую систему уравнений можно представить в матричной форме, обобщив ее для случая схемы с n = y + 1узлами
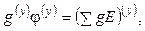
где g(y) – квадратная матрица узловых проводимостей;
φ(y) – матрица-столбец узловых потенциалов;
(ΣgE)(y) – матрица-столбец алгебраических сумм произведений gE.
Общее решение системы линейных алгебраических уравнений порядка y относительно любого из узловых потенциалов, например, потенциала l-го узла можно записать в виде следующего выражения:
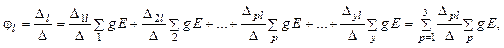где Δ – определитель матрицы узловых проводимостей; Δl – дополнительный определитель, который составляется из определителя Δ за счет замены в нем столбца l столбцом свободных членов; Δpl – алгебраическое дополнение, получаемое из определителя Δ путем исключения столбца l и строки p и умножения получающегося минора на (–1)р+l.
Методика расчета по методу узловых потенциалов.
1. Задаемся положительными направлениями токов в ветвях схемы.
2. Заземляем один из узлов схемы и приравниваем его потенциал нулю.
3. Составляем систему уравнений для определения потенциалов оставшихся узлов. Число уравнений в системе должно быть равно числу узлов минус единица. Каждое уравнение системы составляется для своего узла. В левой части уравнения записывается алгебраическая сумма произведения собственной проводимости узла на потенциал этого узла и произведений смежных проводимостей на потенциалы узлов, связанных ветвями с рассматриваемым узлом. (Собственные проводимости узлов – положительные величины, смежные проводимости - отрицательные величины). В правой части каждого уравнения системы записывается алгебраическая сумма произведений вида gE для ветвей, входящих в рассматриваемый узел и содержащих источники ЭДС. При этом соответствующие gE берутся с плюсом, если источник ЭДС направлен к рассматриваемому узлу, и с минусом, если источник ЭДС направлен от узла.
4. Решается система уравнений, и определяются узловые потенциалы.
5. С помощью закона Ома для участка цепи с источником ЭДС определяются токи ветвей.
Примечания. 1) Собственные и смежные проводимости узлов определяются на основе проводимостей ветвей (не элементов, а ветвей!). Поэтому если ветвь содержит несколько включенных последовательно сопротивлений (в том числе и внутренних сопротивлений источников), то вначале нужно найти результирующее сопротивление ветви как сумму всех последовательно включенных сопротивлений ветви. А затем определить проводимость ветви как величину обратную результирующему сопротивлению ветви. Например, если в первой ветви схемы рис. 27 источник ЭДС не идеальный и характеризуется некоторым внутренним сопротивлением источника Ri1, то результирующее сопротивление первой ветви равно R1 + Ri1, и проводимость первой ветви находится как g1= 1/( R1 + Ri1).
2) При наличии в схеме идеальных источников тока правые части уравнений системы в алгебраических суммах ΣgE будут содержать также токи идеальных источников тока Ik, если ветвь с источником тока входит в рассматриваемый узел. Выбор знака для источника тока такой же, как и для источника ЭДС. Проводимости ветвей, содержащих идеальные источники тока, равны нулю, т.к. внутреннее сопротивление источника тока равно бесконечности.
Метод узловых потенциалов эффективен, если число узлов схемы, уменьшенное на единицу, меньше числа независимых контуров. В противном случае более эффективен метод контурных токов.
Пример 2. Рассчитать токи в ветвях схемы рис. 28 методом узловых потенциалов, вычислить напряжения на зажимах источников, и для контура, содержащего два источника, построить потенциальную диаграмму. Схема характеризуется следующими параметрами: E1 = 40 В, E3 = 30 В, R1 = 4 Ом, R2 = 16 Ом, R3 = 9 Ом, R4 = 8 Ом, R5 = 3 Ом, R6 = 6 Ом, Ri1 = 1 Ом, Ri3 = 1 Ом.
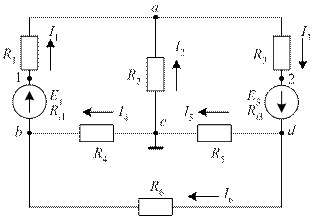
Рис. 28. К примеру расчета методом узловых потенциалов
Решение
Задаемся положительными направлениями токов в ветвях схемы. Заземляем узел c, и приравниваем его потенциал нулю. Определяем проводимости ветвей схемы:
g1= 1/(R1 + Ri1) = 1/(4 + 1) = 0,2 См; g2= 1/R2 =1/16 = 0,0625 См;
g3= 1/(R3 + Ri3) = 1/(9 + 1) = 0,1 См; g4= 1/R4 = 1/8 = 0,125;
g5= 1/R5= 1/3 = 0,3333; g6= 1/R6= 1/6 =0,1667.
Определяем собственные и смежные проводимости узлов:
gaa = g1 + g2 + g3 = 0,2 + 0,0625 + 0,1 = 0,3625 См;
gbb = g1 + g4 + g6 = 0,2 + 0,125 + 0,1667 = 0,4917 См;
gdd = g3 + g5 + g6 = 0,1 + 0,3333 + 0,1667 = 0,6 См;
gab = gba = – g1 = – 0,2 См; gad = gda = – g3 = – 0,1 См;
gbd = gdb = – g6 = – 0,1667 См.
Составляем систему уравнений метода узловых потенциалов:
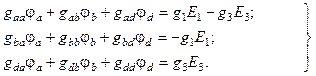
Подставляем в нее численные значения:
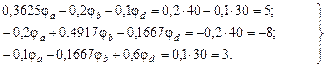
Выполним решение этой линейной алгебраической системы уравнений относительно потенциалов узлов с помощью определителей, причем в отличие от примера 1 рассчитаем дополнительные определители Δa, Δb, Δd непосредственно (без вычисления алгебраических дополнений):
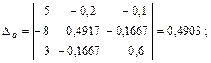
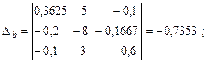
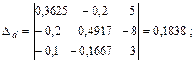
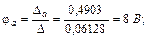
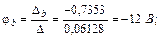
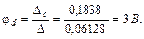
С помощью закона Ома для участка цепи с источником ЭДС определяем токи ветвей:
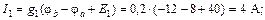
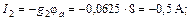
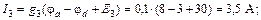
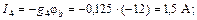
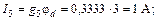
Вычисляем напряжения на зажимах источников:
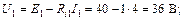
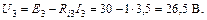
Построим потенциальную диаграмму (рис. 29) для контура cbadc.
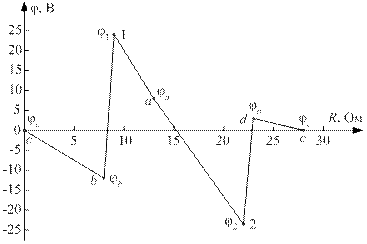
Рис. 29. Потенциальная диаграмма для контура cbadc
Начнем построение из узла c, потенциал которого равен нулю. Потенциалы узлов b, a, d найдены ранее в процессе расчета. Потенциалы промежуточных точек 1 и 2 равны:
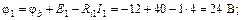
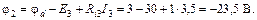
Как видим, при переходе через источник в направлении увеличения ЭДС потенциал возрастает, а при переходе в обратном направлении – убывает.
На потенциальной диаграмме по оси абсцисс откладываем сопротивления соответствующих участков, по оси ординат – потенциалы узлов. Узел c на потенциальной диаграмме расположится в начале координат. Из начала координат по оси абсцисс откладываем в масштабе сопротивление R4 = 8 Ом, а по оси ординат – потенциал φb = –12 В. Из концов соответствующих точек восстанавливаем перпендикуляры к осям, и на их пересечении получаем точку b. Точки c и b на потенциальной диаграмме соединяем отрезком прямой. Далее по оси абсцисс откладываем внутреннее сопротивление первого источника Ri1 = 1 Ом, добавляя его к сопротивлению четвертой ветви, а по оси ординат откладываем из начала координат потенциал φ1 = 24 В. Получаем точку 1. Соединяем ее отрезком прямой с точкой b. Затем по оси абсцисс откладываем сопротивление R1 = 4 Ом, а по оси ординат – потенциал φa = 8 Ом. Получаем точку a. И т.д. до узла c.
Сравним потенциальную диаграмму рис. 29 для замкнутого контура схемы рис. 28 с потенциальной диаграммой рис. 6 для участка электрической цепи, изображенного на рис. 5. Как видим, потенциальная диаграмма рис. 29 замкнутая, а рис. 6 не замкнутая. Кроме того, наклоны отрезков прямых на участках с пассивными элементами на рис. 6 одинаковы, поскольку на участке электрической цепи через все эти элементы течет один и тот же ток. На рис. 29 наклон отрезков прямых на участках с пассивными элементами различен, поскольку эти элементы принадлежат разным ветвям и через них текут разные токи. В схеме рис. 5 источники идеальные. На рис. 6 им соответствуют вертикальные отрезки прямых. В схеме рис. 28 источники реальные. На рис. 29 им соответствуют отрезки прямых b1 и 2d, наклон которых обусловлен наличием внутренних сопротивлений источников.
Дата добавления: 2015-07-24; просмотров: 3288;