Метод наложения
Метод наложения является следствием общефизического принципа наложения (суперпозиции), согласно которому реакция цепи на сумму отдельных воздействий равна сумме реакций цепи на каждое воздействие в отдельности.
В электротехнической практике в качестве воздействий чаще всего выступают ЭДС, а в качестве реакций – токи.
Для обоснования применения принципа наложения к анализу электрической цепи можно использовать формулу (10). В этой формуле отношение Δpq/Δ имеет размерность проводимости (См), а текущий член суммы 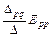 , являющийся произведением проводимости на контурную ЭДС, имеет размерность тока (А) и представляет собой реакцию цепи (частичный ток q-го контура) на контурную ЭДС Epp p-го контура. Поэтому в соответствии с формулой (10) контурный ток равен сумме частичных контурных токов от действия каждой контурной ЭДС в отдельности. Т.е. формула (10) является математическим выражением принципа наложения применительно к контурным токам.
, являющийся произведением проводимости на контурную ЭДС, имеет размерность тока (А) и представляет собой реакцию цепи (частичный ток q-го контура) на контурную ЭДС Epp p-го контура. Поэтому в соответствии с формулой (10) контурный ток равен сумме частичных контурных токов от действия каждой контурной ЭДС в отдельности. Т.е. формула (10) является математическим выражением принципа наложения применительно к контурным токам.
Согласно методу контурных токов контурные ЭДС представляют собой алгебраические суммы ЭДС источников, действующих в рассматриваемом контуре. Токи ветвей являются алгебраическими суммами контурных токов. Поэтому принцип наложения применим и к токам ветвей. А именно: токи ветвей можно рассматривать как алгебраические суммы частичных токов этих же ветвей от поочередного действия каждого из источников электрической энергии в отдельности:
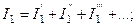
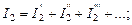
…………………,
где токи с одним, двумя и т.д. штрихами (число штрихов последнего члена каждой суммы равно количеству источников в схеме) – это так называемые частичные токи ветвей.
Методика расчета по методу наложения.
Расчет состоит из f + 1 этапов, где f – количество источников в схеме.
На первом этапе в цепи оставляют только один источник ЭДС или тока. Для остальных источников ЭДС и тока полагают E = 0, Ik = 0 и оставляют только их внутренние сопротивления Ri или проводимости gi. При этом ветви с идеальными источниками тока разрывают, а ветви с идеальными источниками напряжения заменяют короткозамкнутыми перемычками между точками их включения. Далее любым методом (чаще всего с помощью закона Ома) определяют частичные токи I' во всех ветвях схемы от действия оставленного источника. Выбранные условные положительные направления частичных токов в ветвях на схеме обозначают стрелками.
На втором этапе оставляют в цепи второй источник и аналогичным образом определяют частичные токи I" во всех ветвях схемы от действия второго источника, также обозначая на схеме направления действия частичных токов I" стрелками.
И т.д., выполняя на каждом новом этапе расчет частичных токов от действия очередного источника ЭДС или тока.
На последнем этапе определяют токи ветвей как алгебраические суммы частичных токов (с учетом направлений частичных токов в ветвях).
Примечание. Расчет мощностей и энергий можно вести только по полным токам ветвей, т.к. мощности и энергии являются квадратичными функциями токов.
Пример 3. Рассчитать токи в ветвях схемы рис. 31 методом наложения. Схема характеризуется следующими параметрами: E4 = 40 В, E6 = 32 В, Ri4 = 1 Ом, Ri6 = 1 Ом, R1 = 6 Ом, R2 = 10 Ом, R3 = 2 Ом, R4 = 7 Ом, R5 = 8 Ом, R6 = 9 Ом.
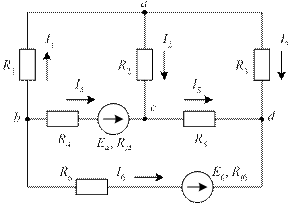
Рис. 31. К методу наложения
Решение
Анализируемая схема является мостовой. В схеме четыре узла и шесть ветвей. В четвертой и шестой ветвях имеются источники с ЭДС E4, E6 и внутренними сопротивлениями источников Ri4, Ri6. Выбранные положительные направления токов ветвей указаны на схеме стрелками.
Расчет токов в рассматриваемой схеме методом наложения необходимо выполнять в три этапа. На первом этапе рассчитаем частичные токи ветвей I' от действия источника в шестой ветви. На втором этапе определим частичные токи ветвей I" от действия источника в четвертой ветви. На третьем этапе найдем результирующие токи ветвей.
Первый этап.Удаляем из схемы ЭДС E4, оставив в схеме внутреннее сопротивление Ri4. Схема приобретает вид, изображенный на рис. 32.
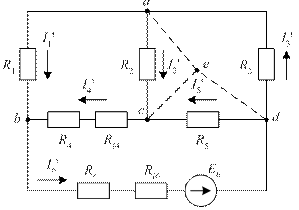
Рис. 32. К первому этапу метода наложения
Заменим контур-треугольник acd эквивалентной звездой (на схеме рис. 32 лучи звезды показаны внутри контура acd пунктиром). Схема приобретает вид, изображенный на рис. 33.
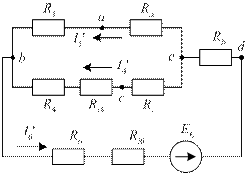
Рис. 33. Схема замещения для первого этапа метода наложения
Для расчета сопротивлений эквивалентной звезды воспользуемся формулами (7):
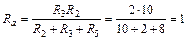 Ом;
Ом; 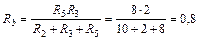 Ом;
Ом;
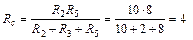 Ом.
Ом.
Схема рис. 33 по структуре соединения ветвей аналогична схеме рис. 16 и представляет собой смешанное соединение в цепи постоянного тока. На схеме рис. 33 первая и четвертая ветви включены параллельно, а шестая ветвь включена последовательно с ними. Определим эквивалентные сопротивления каждой ветви схемы рис. 33.
Первая ветвь
R1a = R1 + Ra = 6 + 1 = 7 Ом.
Четвертая ветвь
R4c = R4 + Ri4 + Rc = 7 + 1 + 4 = 12 Ом.
Шестая ветвь
R6b = R6 + Ri6 + Rb = 9 + 1 + 0,8 = 10,8 Ом.
Применяя формулу (6) для смешанного соединения в цепи постоянного тока, находим входное сопротивление схемы по отношению к ЭДС E6 схемы рис. 33:
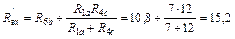 Ом.
Ом.
Далее по закону Ома находим частичный ток шестой ветви
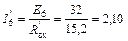 А.
А.
Для определения частичных токов первой и четвертой ветвей рассчитаем напряжение между узлами e и b схемы рис. 33:
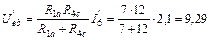 В.
В.
Частичные токи первой и четвертой ветвей находим по закону Ома:
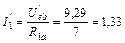 А;
А; 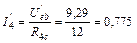 А.
А.
Для нахождения частичных токов второй, третьей и пятой ветвей схемы рис. 32 необходимо рассчитать напряжения 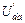 ,
, 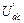 ,
, 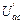 . Расчет выполняем, используя схему рис. 33:
. Расчет выполняем, используя схему рис. 33:
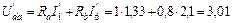 В;
В; 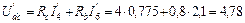 В;
В;
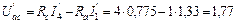 В.
В.
Возвращаемся к схеме рис. 32 и, используя закон Ома для участка цепи, определяем частичные токи второй, третьей и пятой ветвей:
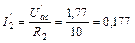 А;
А;  А;
А; 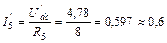 А.
А.
Второй этап. Удалим из исходной схемы (см. рис. 31) ЭДС E6, оставив в схеме внутреннее сопротивление Ri6. Схема приобретает вид, изображенный на рис. 34.
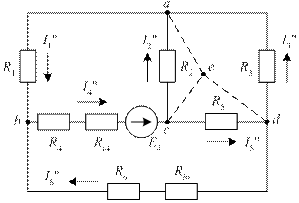
Рис. 34. Ко второму этапу метода наложения
Заменим контур-треугольник acd эквивалентной звездой (на схеме рис. 34 лучи звезды показаны внутри контура acd пунктиром). Схема приобретает вид, изображенный на рис. 35.
Схема рис. 35 – это смешанное соединение в цепи постоянного тока. Численные значения сопротивлений Ra, Rb, Rc эквивалентной звезды схемы рис. 35 те же, что и схемы рис. 33, а именно: Ra = 1 Ом, Rb = 0,8 Ом, Rc = 4 Ом. Поэтому и эквивалентные сопротивления каждой ветви схемы рис. 35 такие же, как и у и схемы рис. 33. Эти сопротивления найдены выше: R1a = = 7 Ом, R4c = 12 Ом, R6b = 10,8 Ом.
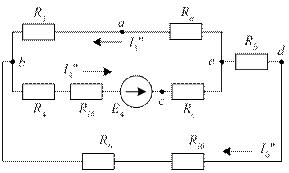
Рис. 35. Схема замещения для второго этапа метода наложения
На схеме рис. 35 первая и шестая ветви включены параллельно, а четвертая ветвь включена последовательно с ними. Применяя формулу (6) для смешанного соединения в цепи постоянного тока, находим входное сопротивление по отношению к ЭДС E4 схемы рис. 35:
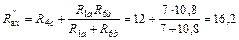 Ом.
Ом.
Далее по закону Ома находим частичный ток четвертой ветви
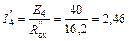 А.
А.
Для определения частичных токов первой и шестой ветвей рассчитаем напряжение между узлами e и b схемы рис. 35:
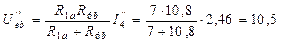 В.
В.
Частичные токи первой и шестой ветвей находим по закону Ома:
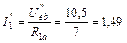 А;
А; 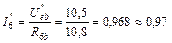 А.
А.
Для нахождения частичных токов второй, третьей и пятой ветвей схемы рис. 34 необходимо рассчитать напряжения 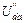 ,
, 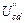 ,
, 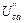 . Расчет выполняем, используя схему рис. 35:
. Расчет выполняем, используя схему рис. 35:
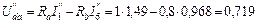 В;
В; 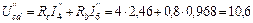 В;
В;
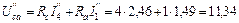 В.
В.
Возвращаемся к схеме рис. 34 и, используя закон Ома для участка цепи, определяем частичные токи второй, третьей и пятой ветвей:
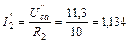 А;
А; 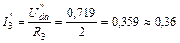 А;
А; 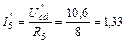 А.
А.
Третий этап. Токи ветвей схемы рис. 31 определяем как алгебраические суммы частичных токов:
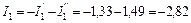 А;
А; 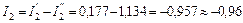 А;
А;
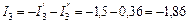 А;
А; 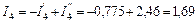 А;
А;
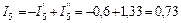 А;
А; 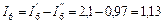 А.
А.
Дата добавления: 2015-07-24; просмотров: 5356;
