Определяем токи ветвей путем алгебраического суммирования контурных токов в каждой ветви.

Примечания. 1) Если ветвь содержит несколько включенных последовательно сопротивлений (в том числе и внутренних сопротивлений источников), то вначале нужно найти результирующее сопротивление ветви как сумму всех последовательно включенных сопротивлений. А затем это результирующее сопротивление ветви использовать для определения собственных и смежных сопротивлений контуров и составления уравнений. Например, если в шестой ветви схемы рис. 24 источник ЭДС не идеальный и характеризуется некоторым внутренним сопротивлением источника R_i6, то результирующее сопротивление шестой ветви будет равно (R₆ + R_i6). Это сопротивление и нужно использовать при составлении уравнений метода контурных токов.

2) При наличии в схеме идеальных источников тока независимые контура следует выбирать так, чтобы токи идеальных источников тока совпадали с контурными токами. Это позволяет уменьшить число уравнений в системе метода контурных токов на число ветвей с идеальными источниками тока.

Метод контурных токов эффективен для схем, у которых число независимых контуров меньше числа узлов, уменьшенного на единицу. В противном случае более эффективен метод узловых потенциалов, который будет рассмотрен в следующем параграфе.

Пример 1. Рассчитать токи в ветвях схемы рис. 25 методом контурных токов. Схема характеризуется следующими параметрами: E₃ = 20 В, R_i3 = 1 Ом, E₄ = 10 В, R_i4 = 1Ом, R₁ = 2 Ом, R₂ = 4 Ом, R₄ = 9 Ом, R₅ = 10 Ом, R₆ = 11Ом.

Решение

Зададимся положительными направлениями токов в ветвях схемы и обозначим эти направления стрелками с символом тока и номером ветви.

Для выбора независимых контуров составим ненаправленный граф рассматриваемой цепи (рис. 26). Дерево графа образуем из второй, третьей и четвертой ветвей. Добавляя к дереву поочередно пятую, шестую и первую ветви, получим в качестве независимых контуров левый и правый верхние контуры и нижний контур исходной схемы.

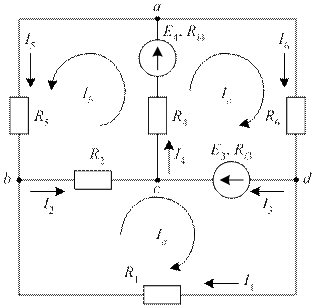
Рис. 25. К примеру расчета методом контурных токов

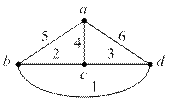
Рис. 26. Ненаправленный граф электрической цепи

Зададимся контурными токами I_a, I_b, I_c, и обозначим их на схеме стрелками (см. рис. 25). Направления контурных токов примем совпадающими с направлениями токов соответственно в пятой, шестой и первой ветвях. На основе второго закона Кирхгофа составляем систему линейных алгебраических уравнений для независимых контуров относительно контурных токов:

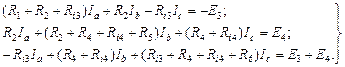
После подстановки в эту систему численных значений имеем:

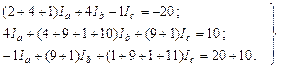
И окончательно:

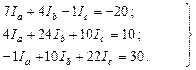
Выполняя решение этой линейной алгебраической системы уравнений относительно контурных токов с помощью определителей с использованием формул (10), (11), получаем:

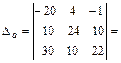
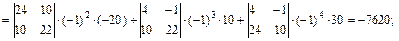
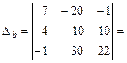
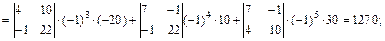
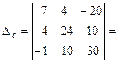
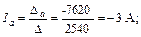
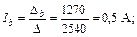
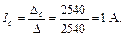
Токи первой, пятой и шестой ветвей совпадают с контурными токами:

I₁ = I_a = – 3 А; I₅ = I_b = 0,5 А; I₆= I_c = 1 А.

Токи второй, третьей и четвертой ветвей определяются путем алгебраического суммирования контурных токов:

I₂ = I_a + I_b = – 2,5 А; I₃ = – I_a + I_c = 4 А; I₄ = I_b + I_c = 1,5 А.