Метод контурных токов

В методе контурных токов вводятся в рассмотрение так называемые контурные токи. Число контурных токов равно числу независимых контуров. Каждый контурный ток замыкается в своем независимом контуре. При этом некоторые ветви схемы будут смежными для нескольких независимых контуров. Через эти ветви замыкается несколько контурных токов. Поэтому токи ветвей представляют собой алгебраические суммы контурных токов.

Следует сразу отметить, что контурные токи являются условными, сугубо расчетными величинами. Однако введение в расчет этих условных токов позволяет упростить нахождение реальных величин – токов ветвей.

В методе контурных токов для независимых контуров составляется система уравнений по второму закону Кирхгофа относительно контурных токов. Число уравнений в системе равно числу независимых контуров. Это число всегда меньше, чем число ветвей в схеме. Число ветвей в схеме равно m, а число независимых контуров и соответственно контурных токов равно [m – (n – 1)], где n – число узлов в схеме. Поэтому число уравнений в методе контурных токов будет меньше, чем в методе законов Кирхгофа.

При составлении системы уравнений метода контурных токов падения напряжений на сопротивлениях схемы в уравнениях второго закона Кирхгофа рассматриваются как алгебраические суммы падений напряжений от всех контурных токов, которые замыкаются через эти сопротивления. Падение напряжения на сопротивлении от контурного тока берется со знаком «плюс», если направление контурного тока совпадает с направлением обхода контура, и со знаком «минус», если направление контурного тока противоположно направлению обхода контура.

Решение системы позволяет найти контурные токи. По ним определяются токи ветвей как алгебраические суммы контурных токов, действующих в данной ветви.

В качестве примера применения метода контурных токов рассмотрим мостовую схему рис. 24, аналогичную той, которую ранее использовали для рассмотрения метода законов Кирхгофа.

В рассматриваемой схеме шесть ветвей. Выбранные условные положительные направления токов ветвей показаны на схеме стрелками, рядом с которыми находятся символы тока I с номерами ветвей, например, I₅.

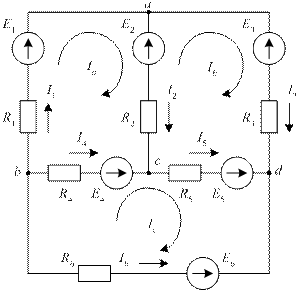
Рис. 24. К методу контурных токов

Схема содержит три независимых контура. В качестве таковых можно рассматривать, например, левый и правый верхние контуры и нижний контур. Пусть в левом верхнем контуре действует контурный ток I_а, в правом верхнем контуре – ток I_b, а в нижнем контуре – ток I_c. Направления действия контурных токов указаны на схеме циклическими стрелками, замыкающимися вдоль каждого из независимых контуров. Рядом со стрелками находятся символы контурных токов I_a, I_b и I_c соответственно. Составляя уравнения второго закона Кирхгофа для независимых контуров, примем направления обхода контуров совпадающими с направлениями действия контурных токов этих контуров. Используя изложенные выше положения метода контурных токов, получим уравнения второго закона Кирхгофа для каждого из трех указанных выше независимых контуров схемы рис. 24.

Левый верхний контур включает в себя первую, вторую и четвертую ветви. В первой ветви действует только один контурный ток: I_a. Поэтому падение напряжения на сопротивлении первой ветви в уравнении второго закона Кирхгофа для левого верхнего контура будет представлено составляющей R₁I_a. Во второй ветви действуют два контурных тока: I_a и I_b. Причем действуют они навстречу друг другу. Направление действия тока I_a совпадает с направлением обхода левого верхнего контура, а направление действия тока I_b противоположно направлению обхода контура. Поэтому падение напряжения на сопротивлении второй ветви в уравнении второго закона Кирхгофа выражается разностью R₂I_a – R₂I_b. В четвертой ветви навстречу друг другу действуют контурные токи: I_a и I_c. Падение напряжения на сопротивлении четвертой ветви в уравнении второго закона Кирхгофа выражается разностью R₄I_a – R₄I_c. В правой части уравнения второго закона Кирхгофа ЭДС Е₁ необходимо взять со знаком «плюс», поскольку направление действия ЭДС Е₁ совпадает с направлением обхода левого верхнего контура. Направления действия источников ЭДС Е₂ и Е₄ противоположны направлению обхода контура. В правой части уравнения второго закона Кирхгофа ЭДС Е₂ и Е₄ необходимо взять со знаком «минус». Таким образом, для левого верхнего контура справедливо следующее уравнение второго закона Кирхгофа, составленное в соответствии с методом контурных токов:

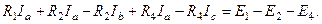
Правый верхний контур образуют вторая, третья и пятая ветви. Во второй ветви навстречу друг другу действуют два контурных тока: I_b и I_a. Направление действия тока I_b совпадает с направлением обхода правого верхнего контура, а направление действия тока I_a противоположно направлению обхода контура. Падение напряжения на сопротивлении второй ветви в уравнении второго закона Кирхгофа для правого верхнего контура выражается разностью R₂I_b – R₂I_a. В третьей ветви действует только один контурный ток: I_b. Падение напряжения на сопротивлении третьей ветви в уравнении второго закона Кирхгофа будет представлено составляющей R₃I_b. В пятой ветви навстречу друг другу действуют два контурных тока: I_b и I_c. Падение напряжения на сопротивлении пятой ветви в уравнении второго закона Кирхгофа для правого верхнего контура выражается разностью R₅I_b – R₅I_c. В правой части уравнения второго закона Кирхгофа ЭДС Е₂ необходимо взять со знаком «плюс», поскольку направление действия ЭДС Е₂ совпадает с направлением обхода контура. Направления действия источников ЭДС Е₃ и Е₅ противоположны направлению обхода контура. В правой части уравнения второго закона Кирхгофа ЭДС Е₃ и Е₅ необходимо взять со знаком «минус». Тогда для правого верхнего контура будет справедливо следующее уравнение второго закона Кирхгофа:

R₂I_b – R₂I_a + R₃I_b + R₅I_b –R₅I_c = E₂ – E₃ – E₅.

Нижний контур включает в себя четвертую, пятую и шестую ветви. В четвертой ветви навстречу друг другу действуют два контурных тока: I_c и I_a. Направление действия тока I_c совпадает с направлением обхода нижнего контура, а направление действия тока I_a противоположно направлению обхода контура. Падение напряжения на сопротивлении четвертой ветви в уравнении второго закона Кирхгофа для нижнего контура выражается разностью R₄I_c – R₄I_a. В пятой ветви навстречу друг другу действуют два контурных тока: I_c и I_b. Падение напряжения на сопротивлении пятой ветви в уравнении второго закона Кирхгофа для нижнего контура выражается разностью R₅I_c – R₅I_b. В шестой ветви действует только один контурный ток: I_c. Падение напряжения на сопротивлении шестой ветви в уравнении второго закона Кирхгофа будет представлено составляющей R₆I_c. В правой части уравнения второго закона Кирхгофа ЭДС Е₄ и Е₅ необходимо взять со знаком «плюс», поскольку направления действия этих источников ЭДС совпадают с направлением обхода контура. Направление действия источника ЭДС Е₆ противоположно направлению обхода контура. В правой части уравнения второго закона Кирхгофа ЭДС Е₆ необходимо взять со знаком «минус». Следовательно, для нижнего контура справедливо следующее уравнение второго закона Кирхгофа:

R₄I_c – R₄I_a + R₅I_c – R₅I_b + R₆I_c = E₄ + E₅ – E₆.

Объединяя уравнения в систему и приводя ее к стандартной форме записи, получаем:

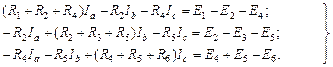
Рассматриваемую систему можно записать и более компактно, введя дополнительные обозначения:

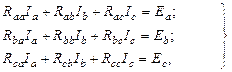(8)

где R_aa = R₁ + R₂ + R₄; R_bb = R₂ + R₃ + R₅; R_cc = R₄ + R₅ + R₆ – собственные сопротивления контуров; R_ab = R_ba = – R₂; R_ac = R_ca = – R₄; R_bc = R_cb = – R₅ – смежные сопротивления контуров; E_a = E₁ – E₂ – E₄; E_b = E₂ – E₃ – E₅; E_c = E₄ + E₅ – E₆ – контурные ЭДС.

Собственные сопротивления контуров всегда положительны, поскольку представляют собой арифметические суммы сопротивлений ветвей, образующих независимый контур. Смежные сопротивления контуров в общем случае являются величинами алгебраическими. Если контурные токи в смежном сопротивлении имеют одинаковое направление, то смежное сопротивление будут положительной величиной. Если контурные токи в смежном сопротивлении имеют встречное направление, то смежное сопротивление будут отрицательной величиной. Например, в рассматриваемой схеме (см. рис. 24) во всех смежных сопротивлениях R₂, R₄, R₅ контурные токи направлены навстречу друг другу. Поэтому в рассматриваемом примере смежные сопротивления отрицательны. Контурные ЭДС определяются как алгебраические суммы всех ЭДС, вошедших в независимый контур. Если направление действия ЭДС совпадает с направлением обхода контура, то соответствующая ЭДС берется в алгебраической сумме со знаком «плюс». Если направление действия ЭДС противоположно направлению обхода контура, то эта ЭДС берется в алгебраической сумме со знаком «минус».

Из решения системы (8) определяются контурные токи, а по ним – токи ветвей как алгебраические суммы контурных токов. В частности, для схемы рис. 24 имеем:

I₁ = I_a; I₂ = I_a – I_b; I₃ = I_b; I₄ = – I_a + I_c; I₅ = – I_b + I_c; I₆= – I_c.

Систему уравнений метода контурных токов можно представить также в матричной форме, обобщив ее для случая схемы c k = [m – (n – 1)] независимыми контурами:

R^(k) I^(k) = E^(k) , (9)

где R^(k) – квадратная матрица контурных сопротивлений (собственных и смежных сопротивлений контуров); I^(k) – матрица-столбец контурных токов; E^(k) – матрица-столбец контурных ЭДС.

Как уже отмечалось ранее, решение системы линейных алгебраических уравнений (9) можно выполнить различными математическими методами.

Используя метод определителей общее решение системы линейных алгебраических уравнений (9) k-го порядка относительно любого из контурных токов, например, q-го контурного тока можно записать в виде следующего выражения:

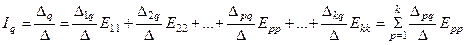. (10)

В формуле (10) определитель Δ системы уравнений (9) имеет вид:

,

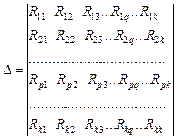где собственные сопротивления контуров имеют идентичные первый и второй индексы и расположены по главной диагонали (главная диагональ проходит из верхнего левого угла определителя в его нижний правый угол), а смежные сопротивления контуров имеют несовпадающие индексы и располагаются симметрично относительно главной диагонали.

Определитель Δ_q для q-го контурного тока в выражении (10) получается из определителя Δ путем замены q-го столбца сопротивлений столбцом свободных членов, составленным из контурных ЭДС:

.

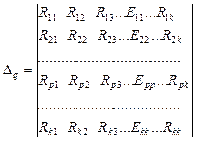Разлагая определитель Δ_q по элементам q-го столбца, имеем:

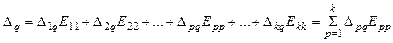, (11)

где E_pp – контурная ЭДС p-го контура; Δ_pq – алгебраическое дополнение, получаемое из определителя Δ путем исключения q-го столбца (номер q соответствует номеру искомого контурного тока) и p-й строки (номер p соответствует номеру контурной ЭДС и меняется поочередно от 1 до k – числа независимых контуров) и умножения получающегося при исключении из определителя q-го столбца и p-й строки минора на (–1)^р+q.

Следует отметить, что для линейных электрических цепей

Δ_pq = Δ_qp.

Действительно, Δ_pq можно получить из определителя Δ путем исключения q-го столбца и p-й строки, а Δ_qp – путем исключения p-го столбца и q-й строки. Определитель Δ характеризуется тем, что R_pq = R_qp. Поэтому в результате исключения из определителя Δ перечисленных столбцов и строк получаются два новых определителя (минора), в которых элементы строк одного равны элементам соответствующих столбцов другого, а такие определители равны друг другу.

Методика расчета по методу контурных токов.