В цепи постоянного тока
В этой схеме два пассивных элемента включены параллельно и один последовательно с ними. Известными величинами в схеме являются входное напряжение U и сопротивления пассивных элементов R1, R2, R3. Требуется определить токи ветвей I1, I2, I3, напряжения U1, U2, мощности отдельных элементов Р1, Р2, Р3 и мощность Р, потребляемую всей схемой.
Анализ схемы выполняют путем ее последовательного упрощения. Сначала определяют эквивалентную проводимость параллельного соединения элементов
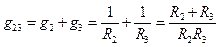
и соответствующее ей эквивалентное сопротивление
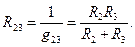
Сопротивление R1 и эквивалентное сопротивление параллельного участка R23 включены последовательно. Поэтому входное сопротивление схемы равно
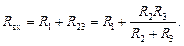 (6)
(6)
Ток I1, потребляемый из сети, находится с помощью закона Ома
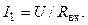
Напряжения U1 и U23 пропорциональны сопротивлениям R1 и R23
U1 = R1I1; U23 = R23I1.
Токи I2 и I3 определяются с помощью закона Ома
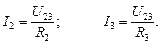
Мощности отдельных элементов и цепи в целом находятся с помощью закона Джоуля-Ленца

Мощность, потребляемая из сети, равна сумме мощностей, потребляемых элементами схемы
Р = Р1 + Р2 + Р3.
При анализе электрических цепей следует иметь в виду, что существуют схемы, в которых нельзя выделить последовательное или параллельное соединение элементов, например, мостовая схема (рис. 17).
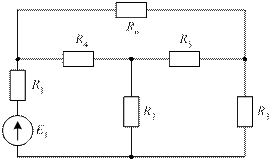
Рис. 17. Мостовая схема
Для нахождения входного сопротивления в такой схеме следует выполнить эквивалентную замену какого-нибудь контура – треугольника на эквивалентную звезду или наоборот. Например, если в схеме рис. 17 верхний треугольник (контур, образованный тремя ветвями) заменить эквивалентной звездой, то получится схема рис. 18. Если внутреннюю звезду (узел, образованный тремя ветвями) схемы рис. 17 заменить эквивалентным треугольником, то получится схема рис. 19.
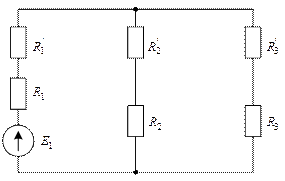
Рис. 18. Эквивалентная схема с заменой треугольника на звезду
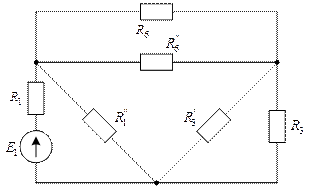
Рис. 19. Эквивалентная схема с заменой звезды на треугольник
Каждая из этих схем эквивалентна исходной схеме рис. 17, так как они потребляют от источника такую же мощность, что и исходная схема. В эквивалентных схемах существуют последовательные и параллельные соединения элементов, и это упрощает нахождение входного сопротивления.
В общем случае преобразование треугольника (рис. 20) в эквивалентную звезду (рис. 21) и наоборот выполняется так, чтобы
1) потенциалы узлов 1, 2, 3 не изменились;
2) токи I1, I2, I3не изменились.
При этом звезда и треугольник будут эквивалентны в энергетическом отношении.
Для преобразования треугольника в эквивалентную звезду и наоборот необходимы формулы для пересчета сопротивлений схем. Получим эти формулы.
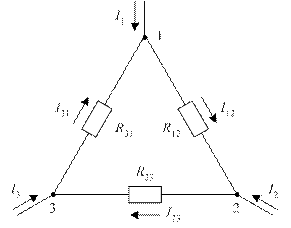
Рис. 20. Схема треугольника
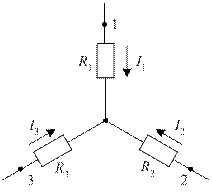
Рис. 21. Схема звезды
Предположим, что схемы рис. 20 и рис. 21 эквивалентны. Если источники одинакового напряжения подключить между точками 1 и 2 этих схем, то от источников потекут одинаковые токи. Значит, входные сопротивления схем одинаковы. В схеме треугольника сопротивления R31 и R23 включены последовательно, а сопротивление R12 включено параллельно с ними. Входное сопротивление треугольника по отношению к зажимам 1 и 2 равно

В звезде сопротивления R1 и R2 включены последовательно. Поэтому входное сопротивление звезды по отношению к зажимам 1 и 2 равно
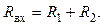
Из равенства входных сопротивлений схем звезды и треугольника следует уравнение

Если рассматривать пары зажимов 2, 3 и 3, 1, то можно получить еще два аналогичных уравнения
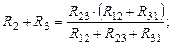
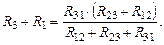
В результате образовалась система из трех уравнений. Если из первого уравнения вычесть второе и прибавить третье, а результат разделить на два, то получится формула для R1. Если из второго уравнения вычесть третье и прибавить первое, а результат разделить на два, то получится формула для R2. И, наконец, если из третьего уравнения вычесть первое и прибавить второе, а результат разделить на два, то получится формула для R3. Окончательно имеем:
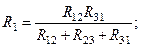
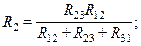
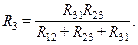 (7)
(7)
Полученные формулы позволяют преобразовать треугольник в эквивалентную звезду.
Решая систему тех же трех уравнений относительно сопротивлений R12, R23, R31, получаем формулы для обратного преобразования звезды в эквивалентный треугольник:
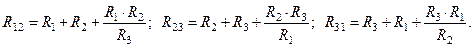
Дата добавления: 2015-07-24; просмотров: 1235;
