Метод эквивалентного генератора

Методом эквивалентного генератора удобно пользоваться, когда требуется определить ток только в одной ветви сложной схемы, а токи в остальных ветвях нас не интересуют. Интересующая нас ветвь в общем случае может быть как линейной, так и нелинейной. Остальная схема обязательно должна быть линейной.

Предположим, нас интересует ток I_q в q-й ветви схемы рис. 38. По отношению к этой ветви остальная цепь представлена активным двухполюсником, внутренняя схема которого нас не интересует.

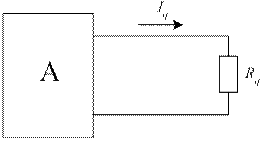
Рис. 38. Активный двухполюсник

Двухполюсник – это схема, из которой выведены два конца. Если внутри двухполюсника есть источник – двухполюсник активный. Если внутри двухполюсника источника нет – двухполюсник пассивный. Пассивный двухполюсник характеризуется одним параметром: входным сопротивлением R_вх. Активный двухполюсник характеризуется двумя параметрами: входным сопротивлением R_вх и напряжением холостого хода на разомкнутых зажимах U_хх. На схемах двухполюсник представляется в виде прямоугольника, из которого выходят два конца. Пассивный двухполюсник обозначается буквой «П», а активный – буквой «А».

Режим работы электрической цепи не изменится, если в q-ю ветвь включить два дополнительных источника ЭДС с равными, но противоположно направленными ЭДС: E' и E" (рис. 39).

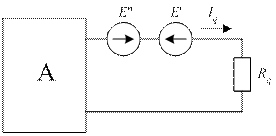
Рис. 39. Активный двухполюсник с двумя дополнительными источниками ЭДС

Воспользуемся методом наложения. Разобьем схему рис. 39 на две (рис. 40а, б) и определим частичные токи этих схем: I_q' и I_q".

а) б)

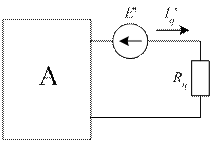
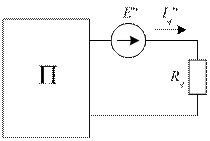
Рис. 40. Активный двухполюсник с источником ЭДС E' (а)

и пассивный двухполюсник с источником ЭДС E" (б)

Частичный ток I_q' обусловлен совместным действием источников активного двухполюсника и источника ЭДС E'. Частичный ток I_q" обусловлен действием источника ЭДС E". В соответствии с этим на рис. 40а двухполюсник активный, а на рис. 40б двухполюсник пассивный.

Предположим, что ЭДС дополнительных источников E' = E" плавно увеличиваются от нуля вверх. При этом ток I_q' начнет уменьшаться и при каком-то значении ЭДС достигнет нуля. Для цепи рис. 40а это будет режимом холостого хода в q-й ветви (I_q' = 0). Напряжение на зажимах q-й ветви будет напряжением холостого хода U_хх активного двухполюсника. Это напряжение будет равно ЭДС E'. Тогда очевидно и в схеме рис. 40б ЭДС E" будет равна напряжению холостого хода активного двухполюсника U_хх. Т.е. мы имеем: E' = E" = U_хх и ток I_q" в схеме рис. 40б будет равен

,

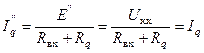где R_вх – входное сопротивление двухполюсника по отношению к зажимам q-й ветви.

Полученное выражение соответствует формуле закона Ома для замкнутой цепи. Поэтому исходную схему (рис. 38) можно заменить эквивалентной ей одноконтурной схемой замкнутой цепи рис. 41, на которой вместо активного двухполюсника представлен эквивалентный источник (эквивалентный генератор) с ЭДС E_эг = U_хх и эквивалентным внутренним сопротивлением, равным входному сопротивлению двухполюсника R_iэг = R_вх .

Название схемы замещения дало название методу расчета: метод эквивалентного генератора.

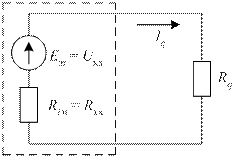
Рис. 41. Схема замещения активного двухполюсника эквивалентным генератором

Методика расчета по методу эквивалентного генератора.

1. Отключаем от схемы исследуемую ветвь.

2. Выполняем анализ схемы с отключенной ветвью и находим напряжение холостого хода между зажимами, соответствующими отключенной ветви.

3. Находим входное сопротивление схемы по отношению к зажимам отключенной ветви. При этом ЭДС источников опускаем, оставляя их внутренние сопротивления, а ветви с идеальными источниками тока размыкаем.

4. Используя формулу метода эквивалентного генератора, находим ток исследуемой ветви.

Рассмотрим примеры применения метода эквивалентного генератора для расчета тока одной из ветвей конкретной схемы.

Пример 4. Дана схема электрической цепи (рис. 42). Параметры схемы известны. Требуется найти ток в пятой ветви методом эквивалентного генератора.

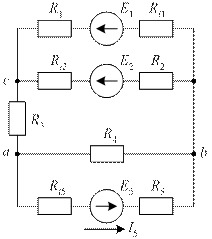
Рис. 42. Схема электрической цепи

Решение

Отключим от схемы пятую ветвь (рис. 43).

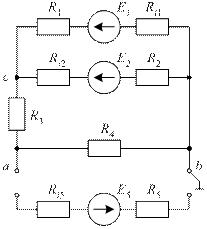
Рис. 43. Схема электрической цепи с отключенной пятой ветвью

В оставшейся схеме опустим ЭДС E₁ и E₂, оставив в схеме сопротивления ветвей и внутренние сопротивления источников (рис. 44).

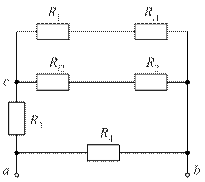
Рис. 44. Схема для расчета входного сопротивления

Находим входное сопротивление схемы (рис. 44) относительно зажимов a и b, учитывая, что первая и вторая ветви схемы включены параллельно, третья ветвь включена последовательно с ними, образуя смешанное соединение ветвей, а четвертая ветвь подключена параллельно со смешанным соединением. Для такой схемы имеем:

.

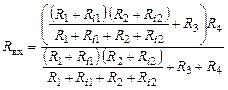Вновь вернемся к рассмотрению схемы (рис. 43) с отключенной пятой ветвью. Заземлим узел b, приравняем потенциал этого узла нулю (φ_b = 0) и найдем напряжение между зажимами a и b схемы при холостом ходе пятой ветви U_abхх методом узловых потенциалов. Имеем следующую систему уравнений:

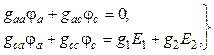
в которой собственные g_aa, g_cc и смежные g_aс = g_ca проводимости узлов a и c выражены через проводимости ветвей схемы

g_aa = g₃ + g₄ ; g_cc = g₁ + g₂ + g₃ ; g_aс = g_сa = – g₃ ;

; ; ; .

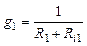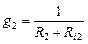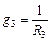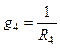Решение системы позволяет найти потенциалы узлов a и c

; .

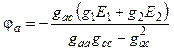Тогда напряжение между зажимами a и b схемы в режиме холостого хода пятой ветви будет равно

U_abхх = φ_a – φ_b = φ_a .

Заменим исходную схему без пятой ветви активным двухполюсником (рис. 45а), а его, в сою очередь, - эквивалентным генератором (рис. 45б).

ЭДС эквивалентного генератора равна напряжению между зажимами a и b в режиме холостого хода пятой ветви E_эг = U_abхх. Внутреннее сопротивление эквивалентного генератора равно входному сопротивлению схемы в режиме холостого хода пятой ветви R_iэг = R_вх.

Тогда в соответствии с методом эквивалентного генератора ток в пятой ветви можно определить, используя формулу закона Ома для замкнутой цепи:

.

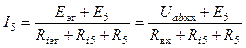А) б)

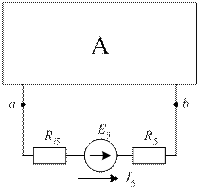
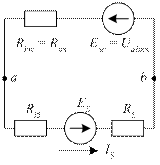
Рис. 45. Схемы замещения: а) с активным двухполюсником;