ЗАКОНОМІРНОСТІ РОЗПОДІЛУ АВТОМОБІЛІВ У ПОТОЦІ

Для оцінки величини пропускної здатності пересічень в одному та декількох рівнях необхідно знати закономірності розподілу інтервалів. Вище зазначалися різні розподіли, які можуть бути використані для моделювання руху потоку автомобілів. Найпростіший з них – розподіл Пуассона, який використовується в дуже вузьких межах значень інтенсивностей руху.

Проведені кандидатом технічних наук Є. М. Лобановим спостереження за характером розподілу інтервалів між автомобілями в різних умовах руху дозволили встановити загальний вигляд функції розподілу інтервалів, характерної для умов руху по дорогах загального користування.

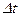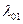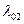Проводячи аналіз кривих розподілу в потоці, можна встановити, що не дивлячись на різний вигляд, ці криві мають спільні точки, розташовані в області малих і великих проміжків (рис. 8.1). При цьому значення та не є чітко фіксованими і абсолютно однаковими для всіх кривих розподілу, а мають деяку розбіжність відносно їх середніх значень, отриману внаслідок неточних вимірювань.

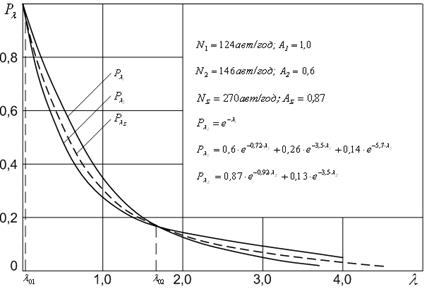
Рис. 8.1. Криві розподілу 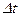в потоці при різній кількості (К) автомобілів, які рухаються повільно: при 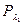К=8,3%; при 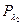К=17,1%; при 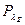К=231,4%.

Параметр 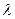в функції розподілу 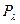означає наступне. Величина 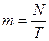є математичним сподіванням кількості автомобілів в даному поперечному січенні дороги за певний проміжок часу. Тоді 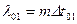; 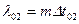є математичним сподіванням кількості автомобілів в даному поперечному січенні дороги за час 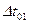та 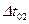. Ймовірність отримання інтервалів 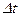> 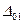та 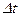> 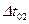для будь-якого потоку (при інтенсивностях руху, коли можливе використання стохастичної моделі) залишається постійним. Це означає, що перерозподіл інтервалів в потоці проходить всередині областей інтервалів розмежованих цими значеннями. Такий перерозподіл отриманий через наступні обставини.

За рахунок еластичності потоку постійно проходить зміна його щільності через перерозподіл автомобілів в різних частинах потоку. Зміна щільності потоку при постійній інтенсивності руху викликає появу додаткових малих інтервалів і розривів в потоці (великі інтервали) відносно попереднього стану потоку. Так як кількість автомобілів в потоці залишається незмінною, то цей перерозподіл можливий лише за рахунок отриманих інтервалів в потоці. 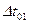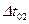Таким чином кількість інтервалів (або ймовірність їх появи) більших за та залишається постійним, так як ущільнення будь-якої частини потоку пов’язане з виникненням розривів в ньому. Інтенсивність ущільнення потоку рівна інтенсивності виникнення розривів.

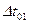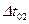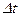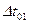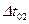Існування характерних інтервалів та означає, що кількість проміжків між автомобілями в середині області , розмежованих та , залишається постійним, але розподіл їх міняється. Величина інтервалів 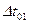та 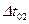змінюється зі зміною інтенсивності руху (рис. 7.2).

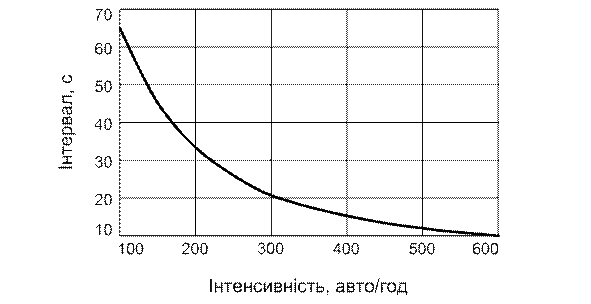
Рис. 7.2. Зміна величини інтервалу 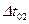в залежності від інтенсивності руху автомобілів.

Як вже було показано, у вільній частині потоку можна спостерігати різні інтервали. Найбільш характерні для цієї частини інтервали великої протяжності, але є і малі інтервали (обгони). Враховуючи, що розподіл інтервалів між автомобілями носить стохастичний характер, доцільно говорити про існування функції розподілу в частині потоку де відбувається вільний рух.