Равновесие в системе, содержащей раствор и кристаллы растворителя

Рассмотрим бинарные системы, в которых вещества неограниченно растворимы друг в друге в жидком состоянии и совершенно нерастворимы в твердом.

По-прежнему будем обозначать величины, относящиеся к растворителю, индексом ₁, а величины, относящиеся к растворенному веществу, индексом ₂.

Если взять жидкий раствор такого типа, то при охлаждении его до определенной температуры начнут выделяться первые кристаллики твердого чистого вещества. Этим веществом является растворитель. Если между первым кристалликом твердого растворителя и раствором устанавливается равновесие, то для его описания используется равенство химических потенциалов

.

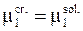Химический потенциал вещества в кристаллике 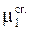соответствует состоянию чистого твердого кристаллического вещества. Его можно обозначить также 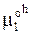. Химический потенциал вещества в растворе m₁^sol зависит от его активности:

.

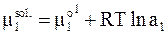Из равенства химического потенциала в равновесно сосуществующих фазах следует

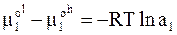. (8 - 17)

Химические потенциалы чистого вещества, входящие в левую часть уравнения (8 - 17), равны значениям энергии Гиббса в этих состояниях (для чистого вещества парциальная молярная величина и просто молярная величина совпадают). Поэтому левая часть уравнения (8 - 17) представляет собой изменение энергии Гиббса при переходе одного моля вещества из твердого состояния в жидкое при температуре кристаллизации раствора. Необходимо отметить, что для плавления чистого растворителя при нормальной температуре кристаллизации изменение энергии Гиббса должно быть равно нулю. В данном случае переход из твердого в жидкое состояние происходит ниже нормальной температуры кристаллизации, и приращение энергии Гиббса при плавлении равно не нулю, а оказывается равным

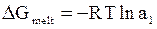. (8 - 18)

Используя уравнение Гиббса - Гельмгольца для данного процесса, получим

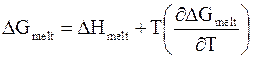; (8 - 19)

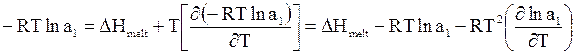
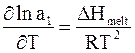. (8 - 20)

Для достаточно узкого диапазона температур теплоту плавления DH_melt можно считать постоянной. В связи с этим интегрирование уравнения (8 - 20) при условии, что стандартной активности растворителя (a₁=1) отвечает стандартная теплота плавления Т^о, дает

;

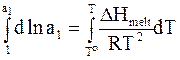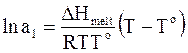. (8 - 21)

Обозначив понижение температуры замерзания раствора по отношению к чистому растворителю DТ и приняв, что температуры Т и Т^о достаточно близки, чтобы заменить произведение ТТ^о на Т^о2, получим

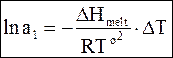. (8 - 22)

Уравнение (8 - 22) позволяет рассчитать термодинамическую активность растворителя по понижению температуры замерзания раствора.

Для разбавленных растворов можно принять

;

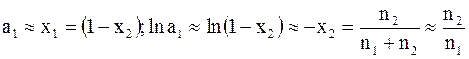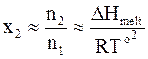. (8 - 23)

Если масса растворителя равна 1000 г, то его количество составляет 1000/M₁ моль. Этому условию отвечает моляльность растворенного вещества m₂.

Не приводя выкладки, подобные использованным в предыдущем параграфе, запишем окончательную форму уравнения

. (8 - 24)

Зависимость между понижением температуры замерзания и содержанием в растворе растворителя также впервые установил Ф. Рауль.

Константа, входящая в уравнение (8 - 24), равна

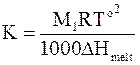. (8 - 25)

Уравнения (8 - 21) и (8 - 24) используются для нахождения термодинамической активности растворителя и моляльности раствора по температуре его замерзания. Этот метод изучения растворов получил название криометрииили криоскопии. Константа К называется криоскопической постоянной.

Уравнение (8 - 24) используется для определения молярных масс веществ по методу криометрии. Для обеспечения достаточной точности определений криоскопическая постоянная растворителя должна быть по возможности большой. Этому условию в наибольшей степени удовлетворяет криоскопическая постоянная камфоры, которая превышает криоскопическую постоянную воды, равную 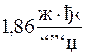, в 21 раз.