Бинарные системы с одним летучим компонентом

Системы такого рода представляют собой раствор нелетучего вещества в летучем растворителе. Традиционно принято обозначать величины, относящиеся к растворителю, индексом ₁, а величины, относящиеся к растворенному веществу, - индексом ₂.

Согласно (6 - 45) летучесть растворителя f₁ связана с его активностью в растворе а₁ соотношением 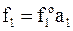, в котором 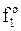- стандартная летучесть растворителя при данной температуре.

При постоянном внешнем давлении летучесть растворителя можно считать постоянной величиной. Поэтому, прологарифмировав равенство, получим

,

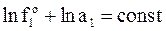а после дифференцирования по температуре имеем

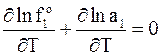. (8 - 9)

Согласно уравнению Клапейрона - Клаузиуса применительно к фазовому переходу из жидкости в пар, рассматриваемый как идеальный газ, производная логарифма давления по температуре равна 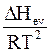, где DH_ev - изменение энтальпии при испарении жидкости. Следовательно, производная логарифма летучести пара над чистым веществом также должна быть равна этой величине

.

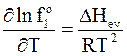С учетом изложенного уравнение (8 - 9) принимает следующий вид:

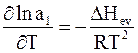. (8 - 10)

Уравнение (8 - 10) можно интегрировать, исходя из следующих условий:

* температурный интервал настолько мал, что энтальпия испарения не зависит от температуры;

* начальным состоянием системы является чистый растворитель, чему соответствуют а₁ = 1 и Т = Т^о (температура кипения чистого растворителя при данном давлении).

Проведем интегрирование:

;

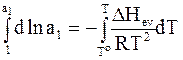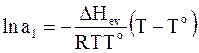. (8 - 11)

Для очень узкого температурного интервала с достаточной точностью можно принять

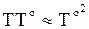. (а)

Обозначим повышение температуры кипения раствора Т по сравнению с чистым растворителем Т^о через DТ:

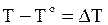. (b)

С учетом (а) и (b) запишем окончательную форму зависимости между термодинамической активностью растворителя и повышением температуры кипения раствора

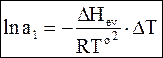. (8 - 12)

Для очень разбавленных растворов можно воспользоваться допущениями: a₁»x₁ и x₂ <<1 (напомним, что х₂ - молярная доля растворенного вещества). В этом случае

.

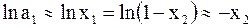Вышеприведенные допущения позволяют установить зависимость между повышением температуры кипения раствора и содержанием в нем растворенного вещества

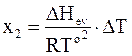. (8 - 13)

Для проведения дальнейших преобразований воспользуемся тем, что в разбавленном растворе число молей растворенного вещества во много раз меньше числа молей растворителя (n₁>>n₂).

Следовательно,

.

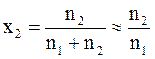Для 1000 г растворителя, молярная масса которого равна М_1, его количество составит 1000/M₁ моль.

Способ выражения концентрации растворенного вещества отношением числа молей его к 1000 г растворителя называется моляльностью, которую обозначают m₂ .

Таким образом, для разбавленных растворов получаем уравнение, связывающее повышение температуры кипения с моляльностью раствора:

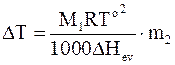. (8 - 14)

В уравнение (8 - 14) входят величины, являющиеся характеристиками растворителя: молярная масса, температура кипения и теплота испарения. Объединив их вместе с универсальной газовой постоянной в общую константу

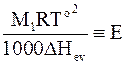, (8 - 15)

получим

. (8 - 16)

Уравнение (8 - 16), впервые экспериментально установленное Ф. Раулем, используется для определения содержания растворенного вещества в растворе по его температуре кипения. От латинского слова ebullio - кипеть произошло название этого метода. Его называют эбулиометриейили эбулиоскопией. Уравнение (8 - 16) называется основным уравнением эбулиометрии. Входящая в уравнение (8 ‑ 16) постоянная называется эбулиометрической постоянной.

Эбулиометрия используется для определения активности растворителя в разнообразных растворах, включая растворы электролитов.