Фазовое равновесие в системе жидкость-пар в двухкомпонентной системе с обоими летучими компонентами

Переменными при построении такого типа диаграмм служат состав, давление и температура.

Для выражения состава наиболее удобно использовать молярные доли компонентов.

Предположим , что система состоит из двух жидкостей А и В, неограниченно растворимых друг в друге. Состав системы можно выразить или молярной долей вещества А, которую обозначим х_А, или молярной долей вещества В, обозначаемой х_В, учитывая, что они связаны соотношением х_А + х_В = 1.

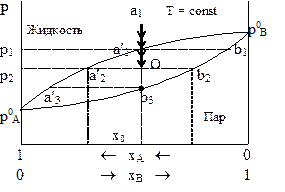Рис. 8 - 3. Фазовая диаграмма для системы с обоими летучими компонентами (Т = const).

Для построения диаграммы на плоскости может быть использован только один переменный внешний параметр. Поэтому существуют два типа диаграмм:

* диаграмма при постоянной температуре с переменными - состав и давление;

* диаграмма при постоянном давлении с переменными - состав и температура.

Вначале рассмотрим принцип построения фазовой диаграммы жидкость ‑ пар при постоянной температуре (рис. 8 - 3).

В зависимости от давления и состава в системе могут находиться или одна фаза (жидкость или пар) или обе равновесные фазы. При больших давлениях система будет находиться в конденсированном состоянии, а при низких - в газообразном. Давление, при котором кипит чистая жидкость А (х_А=1, х_В=0), равно Р^о_А, а давление кипения чистой жидкости В равно Р^о_В.

Взяв систему в жидком состоянии в точке а₁ (см. рис 8 - 3), начнем понижать давление (направление показано стрелками). В точке а₁`_, которой соответствует давление Р₁,жидкость закипает (появляется первый пузырек пара). Состав пара и состав равновесной с ним жидкости окажутся разными.

Общее правило, определяющее различия в составе жидкости и пара, было установлено Д. П. Коноваловым и названо первым законом Коновалова :

Пар богаче жидкости тем компонентом, добавление которого в систему приводит к повышению общего давления.

Обоснование первого закона Коновалова может быть получено из уравнения Гиббса - Дюгема (6 - 20). Для двухкомпонентной системы оно принимает вид:

.

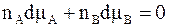Приняв 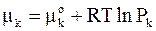, получим 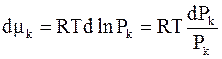, и уравнение Гиббса - Дюгема принимает вид:

.

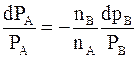Так как отношение чисел молей веществ равно отношению их молярных долей, то получим

.

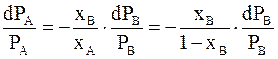В газовой фазе (в данном случае в насыщенном паре) молярная доля вещества равна отношению его парциального давления к общему давлению

,

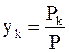из чего следует

;

.

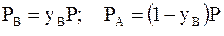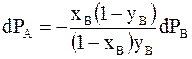Сумма изменения парциальных давлений равна изменению общего давления

.

Разделив обе части равенства на х_В и проведя преобразования, получим

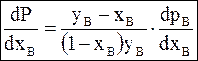. (8 - 6)

С ростом содержания второго компонента х_В давление его пара всегда возрастает. Поэтому производная, входящая в правую часть уравнения (8 - 6), положительна. Производная в левой части равенства может быть положительной при условии у_В - х_В >0, т.е. давление пара в системе возрастает, если содержание компонента в газообразной фазе также возрастает. Если у вещества А равновесное давление пара над чистой жидкостью при данной температуре окажется больше, чем у вещества В, то можно ожидать, что содержание вещества А в газовой фазе окажется больше , чем в жидкой. Состав первого пузырька пара, равновесного с жидкостью при давлении Р₁, обозначим b₁`.

Последующее снижение давления приводит к испарению из жидкости в соответствии с первым законом Коновалова более летучего компонента, в результате чего она вначале будет обогащаться менее летучим веществом В. Однако и газовая фаза по мере снижения давления также начнет обогащаться менее летучим веществом. При давлении Р₂ состав оставшейся жидкости будет соответствовать точке а₂`, а состав накопившегося над ней равновесного с ней пара - точке b<sub>2</sub>. Продолжая снижать давление, можно достичь состояния , в котором в системе останется последняя капля жидкости. Ее состав отвечает точке а<sub>3</sub>`;состав равновесного с ней пара - точкеb₃. При более низком давлении система будет содержать только газовую фазу.

Соединив все точкиа, получим линию жидкости , выше которой в системе отсутствует газовая фаза. Ниже линии, соединяющей точки b, не содержится жидкая фаза. Эта линия называется линией пара .

Между линией пара и линией жидкости находится двухфазная область, содержащая как пар, так и жидкость.

Выше линии жидкости и ниже линии пара система условно бивариантна. Это означает, что система имеет две степени свободы при условии, что один из внешних параметров принимается постоянным. В дальнейшем, описывая плоские фазовые диаграммы, мы будем опускать слово «условно».

Между обеими линиями система моновариантна. Формально этот результат следует из правила фаз Гиббса. Действительно, в первых двух случаях (однофазная система с одним переменным внешним параметром) имеем

f = K - F + 1 = 2 - 1 + 1 = 2, а последнему случаю (двухфазная система) отвечает f = 2 - 2 + 1 = 1.

Внешне кажется, что в последнем случае одновременно изменяются и молярная доля и давление. Однако это впечатление обманчиво. Перемещение параллельно оси абсцисс не изменяет состав равновесных фаз, хотя именно им определяется равновесие. В любой точке на линиях, соединяющих точку а₁ с точкой b₁, точку а₂ с точкой b₂ и т.д., состав фаз определяется только крайними точками, т.е. остается фиксированным. Перемещение вдоль оси состава означает только изменение соотношения числа молей обеих фаз. По данным, представленным на диаграмме, можно найти это соотношение. Для этого обозначим число молей жидкой фазы n^l , а равновесного с ней пара - n^v.

Число молей вещества А в жидкости равно

,

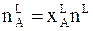где 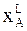- молярная доля вещества А в жидкости .

Соответственно число молей вещества В в жидкости , число молей вещества А в газовой фазе и вещества В в газовой фазе равны

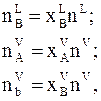
где 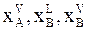- молярные доли вещества А в газовой фазе и вещества В в жидкой и газовой фазе.

В точке О, находящейся между линиями жидкости и пара, средняя мольная доля вещества А в системе равна х_О, из чего следует

.

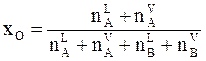или

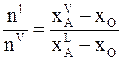. (8 - 7)

Равенство (8 - 7) отражает «правило рычага» , согласно которому

отношение количества веществ в жидкой фазе к количеству веществ в газовой фазе в точке между линиями пара и жидкости равно отношению длины горизонтального отрезка, соединяющего данную точку с линией пара, к длине горизонтального отрезка, соединяющего точку с линией жидкости.

Если при построении диаграммы использовать не молярные, а массовые доли, то правило рычага позволит определить отношение масс фаз, которое также обратно пропорционально отношению длин отрезков, соединяющих выбранную точку с линиями соответствующих фаз.

Кроме диаграммы состав - давление (при постоянной температуре), можно построить диаграмму состав - температура кипения (при постоянном давлении).

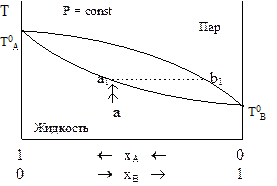Рис. 8 - 4.Диаграмма температура-состав для систем с обоими летучими компонентами.

При построении этой диаграммы (рис. 8 - 4) вначале отложим температуры кипения чистых жидкостей ТА^о и ТВ^о. Низким температурам отвечает конденсированное состояние системы, а высоким - газообразное. Взяв жидкую систему в точке а при низкой температуре, начнем ее нагревать. Повышение температуры жидкости показано стрелками. В точке а₁ появляется первый пузырек пара, что означает начало кипения жидкости. Как и в предыдущем случае, состав жидкого раствора двух летучих компонентов и равновесного с ним пара отличаются по составу. Первый закон Коновалова можно модифицировать, придав ему более удобную для данного случая формулировку:

Пар богаче жидкости тем компонентом, добавление которого к системе понижает температуру кипения.

При построении диаграммы состав - температура подобно диаграмме состав - давление выделяют линии жидкости и пара. Ниже линии жидкости находится гомогенная жидкая система с двумя степенями свободы. Выше линии пара - гомогенная газообразная система. Между ними - двухфазная система, отношение количеств вещества в фазах или отношение масс фаз в которой определяется по правилу рычага.

Заметим, что для одной и той же пары веществ обе диаграммы имеют подобную форму. Различие между ними заключается в том, что жидкости с большим давлением пара на диаграмме состав - давление отвечает меньшая температура кипения на другой диаграмме.