Правило фаз Гиббса. Правило фаз Гиббса устанавливает зависимость между числом степеней свободы, числом компонентов, числом фаз и числом внешних параметров системы.

Правило фаз Гиббса устанавливает зависимость между числом степеней свободы, числом компонентов, числом фаз и числом внешних параметров системы.

В соответствии с данным выше определением число степеней свободы, или вариантность, системы f равно разности между числом изменяемых факторов системы Var и числом уравнений, связывающих между собой эти факторы Eq:

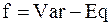
Если система содержит Ф фаз и К компонентов, то в каждой фазе можно изменять К-1 величину, определяющую ее состав.

У читателя может возникнуть вопрос: почему эта величина не равна К? Для ответа на этот вопрос рассмотрим следующий несложный пример. Раствор (гомогенная система) содержит 3% хлорида натрия, 2% уксусной кислоты, 3,5% глюкозы и воду. Содержание воды можно не указывать, так как оно определяется содержанием остальных компонентов и оказывается уже заданной ими величиной.

Поскольку в каждой фазе может изменяться содержание К-1 компонента, то во всех Ф фазах число изменяемых величин, определяющих их состав, окажется равным Ф(К-1). Кроме этих величин, в системе может изменяться r внешних параметров. Поэтому общее число изменяемых величин составит

.

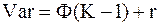Число уравнений между этими величинами можно установить, применяя основное свойство химического потенциала: химические потенциалы компонента, содержащегося в разных фазах, равны

m₁^(I)=m₁^(II); m₁^(I)=m₁^(III) ; ... ...m₁^(I)=m₁^(F) ;

m₂^(I)=m₂^(II); m₂^(I)=m₂^(III); ... ...m₂^(I)=m₂^(F) ;

.... ... ....

... ... ...

m_k^(I)=m_k^(II);m_k^(I)=m_k^(III);... ...m_k^(I)=m_k^(F) .

Приведенная система уравнений состоит из К строк, в каждой из которых Ф-1 уравнение. Таким образом, общее число уравнений связи равно

.

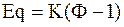Получаем окончательную форму уравнения для числа степеней свободы

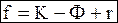(8 - 5)

Уравнение (8 - 5) выражает правило фаз Гиббса , согласно которому

число степеней свободы системы равно числу компонентов и числу изменяемых внешних параметров минус число фаз.