Уравнения состояния

Все параметры, включая температуру, зависят друг от друга. Эта зависимость выражается уравнениями типа

F(X₁,X₂,...,x₁,x₂,...,T) = 0,

где Х₁,Х₂,... - обобщенные силы, х₁,х₂,... - обобщенные координаты, а Т - температура. Уравнения, устанавливающие зависимость между параметрами, называются уравнениями состояния.

Уравнения состояния приводятся для простых систем, преимущественно - для газов. Для жидкостей и твердых тел, принимаемых, как правило, несжимаемыми, уравнения состояния практически не предлагались.

К середине ХХ в. было известно значительное число уравнений состояния для газов. Однако развитие науки пошло таким путем, что почти все они не нашли применения. Единственное уравнение состояния, которое продолжает широко использоваться в термодинамике, - уравнение состояния идеального газа.

Идеальным газомназывается газ, приближающийся по свойствам к газу низкомолекулярного вещества, находящегося при очень низком давлении и сравнительно высокой температуре (достаточно далекой от температуры конденсации).

Для идеального газа выполняются:

· закон Бойля - Мариотта(при постоянной температуре произведение давления газа на его объем остается постоянным для данного количества вещества)

PV=const,

· закон Гей-Люссака(при постоянном давлении отношение объема газа к температуре остается постоянным)

,

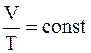· закон Шарля(при постоянном объеме отношение давления газа к температуре остается постоянным)

.

С. Карно объединил перечисленные выше соотношения в единое уравнение типа

.

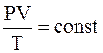Б. Клапейрон придал этому уравнению форму, близкую к современной:

PV=RT .

Объем V, входящий в уравнение состояния идеального газа, относится к одному молю вещества. Его называют также молярным объемом.

Общепринятое название постоянной R - универсальная газовая постоянная (очень редко можно встретить название «постоянная Клапейрона»). Значение ее составляет

R=8,31431Дж/моль×К.

Приближение реального газа к идеальному означает достижение настолько больших расстояний между молекулами, при которых можно полностью пренебречь их собственным объемом и возможностью взаимодействия, т.е. существования сил притяжения или отталкивания между ними.

Ван-дер-Ваальс предложил уравнение, учитывающее эти факторы, в следующей форме:

,

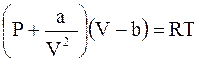где a и b - постоянные, определяемые для каждого газа отдельно. Остальные величины, входящие в уравнение Ван-дер-Ваальса, имеют тот же смысл, что и в уравнении Клапейрона.

Возможность существования уравнения состояния означает, что для описания состояния системы можно указывать не все параметры, а их число, меньшее на единицу, так как один из них может быть определен (хотя бы гипотетически) из уравнения состояния. Например, для описания состояния идеального газа достаточно указать только одну из следующих пар: давление и температуру, давление и объем, объем и температуру.

Объем, давление и температуру иногда называют внешними параметрами системы.

Если допускается одновременное изменение объема, давления и температуры, то система имеет два независимых внешних параметра.

Система, находящаяся в термостате (устройстве, обеспечивающем постоянство температуры) или маностате (устройстве, обеспечивающем постоянство давления), имеет один независимый внешний параметр.

Глава 1. Первое начало термодинамики