Термодинамика гальванического элемента
В квазистатическом процессе, который осуществляется при очень высоком электрическом сопротивлении внешней части цепи или при работе с другим источником, развивающим равную, но противоположно направленную электродвижущую силу, то есть при почти нулевом электрическом токе в цепи полезная работа гальванического элемента определяется равенством
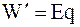 , (1 - 1)
, (1 - 1)
в котором E - электродвижущая сила (ЭДС) элемента, q - переносимый заряд.
Если в гальваническом элементе протекает реакция
n1A1 + n2A2 + ...+ni Ai + ...= n¢1B1 + n¢2B2 +... + n¢jBj +...,
то ее полезная работа в пересчете на количества превращаемых веществ, равных стехиометрическим коэффициентам, совпадает с полезной работой
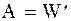 . (1 - 2)
. (1 - 2)
Переносимый по цепи заряд определяется произведением числа электронов, переносимых от ионов, атомов или молекул окисляемого вещества к ионам, атомам или молекулам восстанавливаемого вещества z, на заряд одного электрона e. Так как при использовании сродства количество веществ выражается в молях, то это произведение необходимо умножить на постоянную Авогадро NA.
Таким образом,
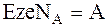 . (1 - 3)
. (1 - 3)
Принимая во внимание, что произведение заряда одного электрона на постоянную Авогадро равно постоянной Фарадея F, то выражению для ЭДС гальванического элемента можно придать следующий вид:
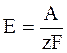 . (1 - 4)
. (1 - 4)
Для многократно рассматривавшейся реакции
Cu2+ + Zn = Cu + Zn2+
z=2, так как от атома цинка к иону меди переносятся два электрона.
В более сложном примере для реакции
2KMnO4 + 10FeSO4 + 8H2SO4 = 5Fe2(SO4)3 + 2MnSO4 + K2SO4 + 8H2O
(2 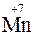 + 10
+ 10 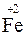
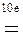 10
10 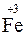 + 2
+ 2 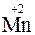 )
)
(нижняя запись показывает изменение степени окисления элементов) число переносимых зарядов составит 10F.
Используя традиционную форму записи выражения для сродства химической реакции (см. часть 1 «Курса физической химии», стр. 76),
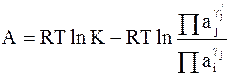 , (1 - 5)
, (1 - 5)
в котором K - константа равновесия, a1, a2, ...,ai,... - активности веществ, n1,n2,... ...,ni, ...,nj... - стехиометрические коэффициенты, получим выражение для ЭДС гальванического элемента:
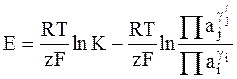 . (1 - 6)
. (1 - 6)
В стандартном состоянии термодинамические активности равны 1 и правый член выражения (1 - 6) обращается в нуль. Следовательно, ЭДС для стандартных условий (она также называется стандартной ЭДС) находится по формуле
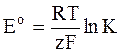 . (1 - 7)
. (1 - 7)
В электрохимии принято записывать уравнения со знаком «плюс» перед вторым членом. С учетом этой особенности и выражения (1 - 7) окончательная форма уравнения для ЭДС принимает следующий вид:
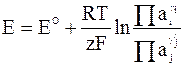 . (1 - 8)
. (1 - 8)
Уравнение (1 - 8) называется уравнением Нернста.
Дата добавления: 2015-07-22; просмотров: 795;
