Уравнение (2.3.1) называется волновым уравнением.
Непосредственной подстановкой легко убедиться в том, что волновому уравнению удовлетворяют не только уравнения волн (2.2.14) и (2.2.20), но и любая функция вида
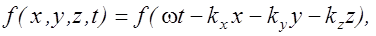 (2.3.2)
(2.3.2)
описывающая некоторую волну.
Уравнение (2.3.1) может быть записано более компактно с помощью оператора Лапласа
D= 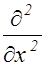 +
+ 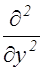 +
+ 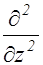 . (2.3.3)
. (2.3.3)
С учетом выражения (2.3.3) волновое уравнение (2.3.1) принимает вид:
Dx 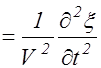 . (2.3.4)
. (2.3.4)
Основным следствием теории Максвелла был вывод о существовании электромагнитных волн. Все электромагнитные явления могут быть объяснены с помощью уравнений Максвелла:
 (2.3.5)
(2.3.5)
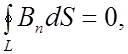 (2.3.6)
(2.3.6)
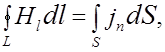 +
+ 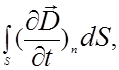 (2.3.7)
(2.3.7)
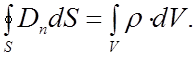 (2.3.8)
(2.3.8)
Кратко напомним физический смысл уравнений (2.3.5)-(2.3.8). Уравнение (2.3.5) является обобщением закона электромагнитной индукции и поясняет гипотезу Максвелла о возникновении вихревого электрического поля за счет изменяющегося магнитного поля. Уравнение (2.3.6) отражает вихревой характер магнитного поля (силовые линии замкнуты), а также указывает на отсутствие магнитных зарядов.
Магнитное поле может быть создано как движущимися зарядами, так и за счет изменяющегося электрического поля, уравнение (2.3.7). Из уравнения (2.3.8) следует, что источником электрического поля могут быть заряды, причем силовые линии вектора 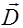 начинаются и заканчиваются на них (или уходят в бесконечность).
начинаются и заканчиваются на них (или уходят в бесконечность).
Уравнения (2.3.5) - (2.3.8) называют уравнениями Максвелла в интегральной форме, так как они связывают усредненные характеристики поля в пределах объема, охватываемого поверхностью, через которую определяется поток, или в окрестности контура, по которому берется циркуляция. Уменьшая размеры поверхности или контура (стягивая их в точку), можно перейти к уравнениям в дифференциальной форме, которые связывают характеристики поля в каждой точке пространства.
Для описания свойств векторных полей вводится векторная функция точки rot 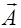 (читается ротор вектора
(читается ротор вектора 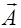 ), которая определяется выражением
), которая определяется выражением

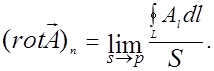 (2.3.9)
(2.3.9)
Под (rot 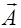 n) подразумевается проекция вектора rot
n) подразумевается проекция вектора rot 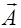 на положительную
на положительную 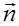 нормаль к площадке S, охватываемой контуром L (рис. 2.3.1).
нормаль к площадке S, охватываемой контуром L (рис. 2.3.1).

|
Определение (2.3.9) не зависит от выбора системы координат, поэтому, выбирая ориентации площадки S в плоскостях yx, xz, xy, получим, соответственно, ориентации нормали, совпадающие с осями x, y, z, и, следовательно, с помощью выражения (2.3.9) можно найти проекции вектора rot 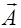 на оси декартовой системы координат. Соответствующий расчет показывает, что эти проекции определяются выражениями:
на оси декартовой системы координат. Соответствующий расчет показывает, что эти проекции определяются выражениями:
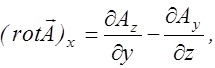 (2.3.10)
(2.3.10)
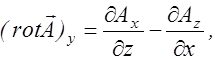 (2.3.11)
(2.3.11)
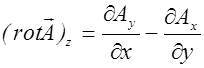 . (2.3.12)
. (2.3.12)
Запись формул векторного анализа существенно упрощается, если использовать векторный дифференциальный оператор набла (оператор Гамильтона)
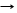 Ñ=
Ñ= 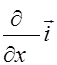 +
+ 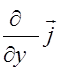 +
+ 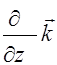 , (2.3.13)
, (2.3.13)
где 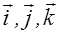 - орты декартовой системы координат.
- орты декартовой системы координат.
Нетрудно убедиться, что вектор rot 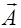 может быть представлен как векторное произведение векторов
может быть представлен как векторное произведение векторов 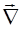 и
и 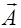 :
:
rot 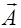 =
= 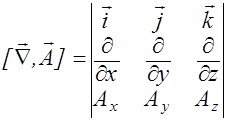 . (2.3.14)
. (2.3.14)
Действительно, из уравнений (2.3.10)-(2.3.12) и выражения (2.3.14) получается одно и то же разложение вектора rot 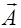 по осям декартовой системы координат:
по осям декартовой системы координат:
rot 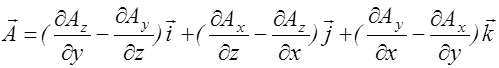 . (2.3.15)
. (2.3.15)
Кроме векторной функции точки rot 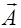 , используется и скалярная функция точки div
, используется и скалярная функция точки div 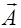 (читается дивергенция вектора
(читается дивергенция вектора 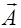 ), общее определение которой дается выражением
), общее определение которой дается выражением

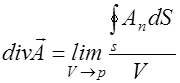 . (2.3.16)
. (2.3.16)
 Интеграл берется по произвольной замкнутой поверхности S, охватывающей объем V (рис.2.3.2).
Интеграл берется по произвольной замкнутой поверхности S, охватывающей объем V (рис.2.3.2).
Можно показать, что дивергенция вектора 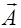 равна скалярному произведению вектора
равна скалярному произведению вектора 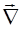 на вектор
на вектор 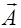
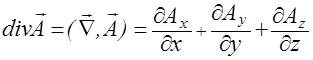 . (2.3.17)
. (2.3.17)
Стягивая в точку контуры, по которым берутся циркуляции, и поверхности, через которые определяются потоки, в уравнениях (2.3.5)-(2.3.8), можно получить уравнения Максвелла в дифференциальной форме:
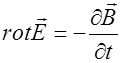 , (2.3.18)
, (2.3.18)
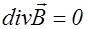 , (2.3.19)
, (2.3.19)
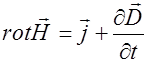 , (2.3.20)
, (2.3.20)
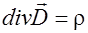 . (2.3.21)
. (2.3.21)
При решении уравнений (2.3.18)-(2.3.21) используются соотношения между входящими в них величинами:
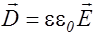 , (2.3.22)
, (2.3.22)
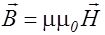 , (2.3.23)
, (2.3.23)
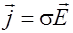 . (2.3.24)
. (2.3.24)
Для однородной нейтральной (r = 0) непроводящей ( 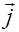 =0) среды уравнения (2.3.18)-(2.3.21), с учетом соотношений (2.3.22)-(2.3.24), принимают вид
=0) среды уравнения (2.3.18)-(2.3.21), с учетом соотношений (2.3.22)-(2.3.24), принимают вид
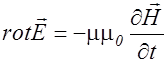 , (2.3.25)
, (2.3.25)
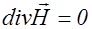 , (2.3.26)
, (2.3.26)
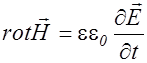 , (2.3.27)
, (2.3.27)
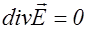 . (2.3.28)
. (2.3.28)
Применим к уравнению (2.3.25) операцию rot
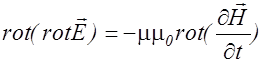 . (2.3.29)
. (2.3.29)
В правой части уравнения (2.3.29), изменяя порядок дифференцирования по координатам и времени, получаем
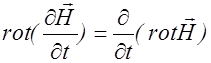 . (2.3.30)
. (2.3.30)
С учетом уравнения (2.3.27) и выражения (2.3.30) уравнение (2.3.29) можно записать в виде
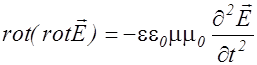 . (2.3.31)
. (2.3.31)
Произведя аналогичные преобразования с уравнением (2.3.27), получаем уравнение
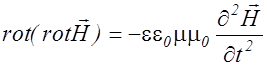 . (2.3.32)
. (2.3.32)
Операцию 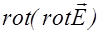 можно представить в соответствии с (2.3.14) как двойное векторное произведение
можно представить в соответствии с (2.3.14) как двойное векторное произведение
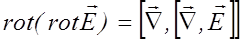 . (2.3.33)
. (2.3.33)
В соответствии с правилами дифференцирования и формулой для двойного векторного произведения
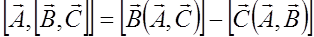
получаем (2.3.33) в виде
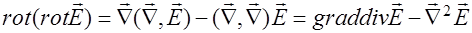 .
.
С учетом выражений (2.3.28) и (2.3.34), уравнение (2.3.31) принимает вид:
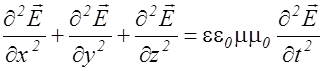 . (2.3.34)
. (2.3.34)
Выполняя аналогичные преобразования, уравнение (2.3.32) можно привести к виду
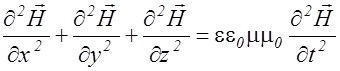 . (2.3.35)
. (2.3.35)
Необходимо отметить, что уравнения (2.3.34) и (2.3.35) связаны друг с другом, так как они получены из уравнений (2.3.31) и (2.3.32)в каждое из которых входят векторы 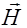 и
и 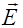 .
.
Из сравнения уравнений (2.3.34) и (2.3.35) с волновым уравнением (2.3.1) следует, что они описывают электромагнитную волну, распространяющуюся с фазовой скоростью
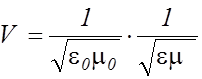 . (2.3.36)
. (2.3.36)
Интересно отметить, что в вакууме (e = 1,m = 1) фазовая скорость принимает значение
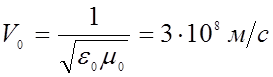 ,
,
то есть, равна скорости света.
Таким образом, из уравнений Максвелла (2.3.18)-(2.3.21) получены волновые уравнения (2.3.34) и (2.3.35), решения которых описывают электромагнитную волну. Для плоской электромагнитной волны, распространяющейся вдоль оси z решения уравнений (2.3.34) и (2.3.35) имеют вид:
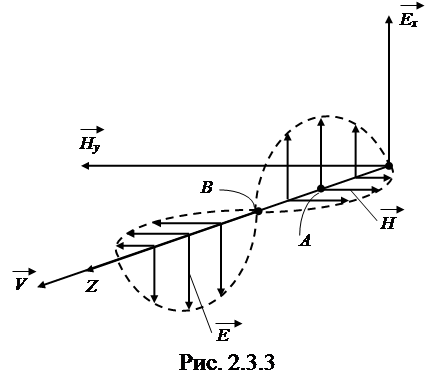 |
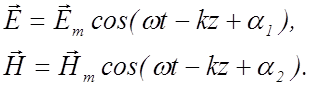 (2.3.37)
(2.3.37)
Моментальная “фотография” такой волны представлена на рис. 2.3.3, из которого следует, что векторы 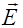 и
и 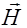 взаимно перпендикулярны и образуют с направлением распространения (ось z) правовинтовую систему. Из ортогональности векторов
взаимно перпендикулярны и образуют с направлением распространения (ось z) правовинтовую систему. Из ортогональности векторов 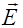 и
и 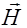 , и направления распространения волны следует, что электромагнитная волна поперечна.
, и направления распространения волны следует, что электромагнитная волна поперечна.
Установим соотношения между начальными фазами колебаний векторов 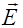 и
и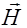 и их амплитудами Еm и Нm. Учитывая ориентации векторов
и их амплитудами Еm и Нm. Учитывая ориентации векторов 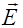 и
и 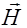 (рис. 2.33) уравнение плоской волны можно записать в виде:
(рис. 2.33) уравнение плоской волны можно записать в виде:
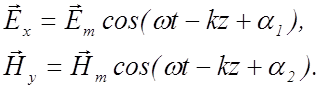 (2.3.38)
(2.3.38)
Запишем уравнения Максвелла (2.3.25) и (2.3.27) в проекциях на оси х, у, z (2.3.10-2.3.12):
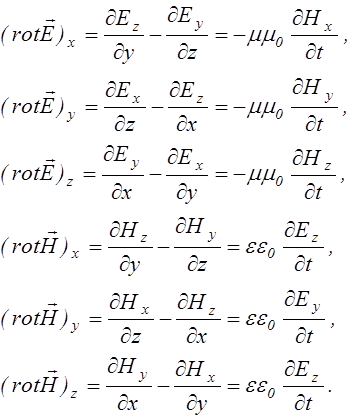 (2.3.39)
(2.3.39)
Для рассматриваемой волны Еy=Еz=0 и Нx=Нz=0, поэтому из системы уравнений (2.3.39) остается только два уравнения:
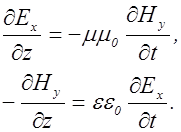 (2.3.40)
(2.3.40)
Подставляя в уравнения (2.3.40) функции (2.3.38), получим уравнения:
kEm sin(wt-kz+a1)=-m m0Hmw sin(wt-kz+a2),
kHm sin(wt-kz+a2)=-ee0Emw sin(wt-kz+a1). (2.3.41)
Для того, чтобы уравнения (2.3.41) удовлетворялись необходимо выполнение равенств:
kEm = -m m0Hmw,
kHm = -ee0Emw , (2.3.42)
a1=a2.
Перемножая первые два равенства, получим
ee 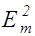 w=m m0
w=m m0 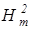 w, (2.3.43)
w, (2.3.43)
откуда 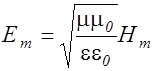 . (2.3.44)
. (2.3.44)
Если волна распространяется в вакууме (e=1, m=1) расчет по формуле (2.3.44) дает
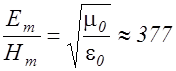 .
.
Дата добавления: 2015-07-22; просмотров: 847;
