Уравнение плоской и сферической волн. Длина волны, волновое число, фазовая скорость
Уравнением волны называется выражение, которое определяет смещение 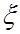 колеблющейся точки как функцию координат x, y, z ее равновесного положения и времени t:
колеблющейся точки как функцию координат x, y, z ее равновесного положения и времени t:
x =x(x, y, z, t). (2.2.1)
Найдем явный вид функции x для плоской волны, считая что колебания носят гармонический характер. Направим ось х вдоль направления распространения волны, тогда волновые поверхности будут перпендикулярны к оси х. Так как все точки, принадлежащие волновой поверхности, колеблются одинаково, то смещение x будет зависеть только от х и t:
x = x (x,t). (2.2.2.)
Пусть колебания точек, лежащих в плоскости х = 0
(рис. 2.2.1), описываются гармонической функцией:
x(0,t) = Acoswt. (2.2.3)
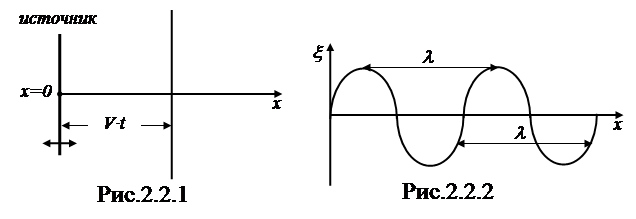 |
Частицы среды расположенные слева и справа от источника будут совершать гармонические колебания, смещения которых в некоторый момент времени t можно представить графиком (рис.2.2.2).
Кратчайшее расстояние между частицами, колеблющимися одинаковым образом (в одинаковой фазе), называется длиной волны l. Длина волны, очевидно, равна расстоянию, на которое распространяется волна за период колебаний частиц:
l = V.T. (2.2.4)
Учитывая связь периода колебаний T с частотой n, получим, что
ln=V. (2.2.5)
Найдем уравнение колебаний частиц в плоскости, соответствующей произвольному значению x (это и будет уравнение плоской волны).
Для того чтобы пройти путь от плоскости x = 0 до плоскости, соответствующей значению x, волна затратит время
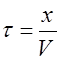 ,
,
где V - скорость распространения волны.
Следовательно, колебания частиц в плоскости x будет отставать по времени на t от колебаний частиц в плоскости x=0, то есть уравнение колебаний будет иметь вид:
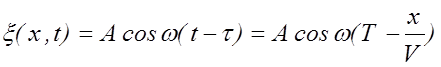 . (2.2.6)
. (2.2.6)
Таким образом, уравнение плоской волны имеет вид:
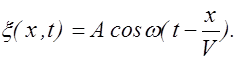 (2.2.7)
(2.2.7)
При получении уравнения (2.2.7) изменение амплитуды колебаний не учитывалось, то есть это уравнение справедливо, если энергия волны не поглощается средой.
Найдем скорость распространения волны. Для этого зафиксируем значение фазы в уравнении (2.2.7), то есть положим:
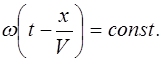 (2.2.8)
(2.2.8)
Это выражение определяет координату x, для которой зафиксированное значение фазы достигается в данный момент времени t. Определив из (2.2.8) значение 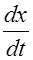 , найдем скорость, с которой перемещается данное значение фазы - фазовую скорость. Продифференцируем выражение (2.2.8), тогда получим:
, найдем скорость, с которой перемещается данное значение фазы - фазовую скорость. Продифференцируем выражение (2.2.8), тогда получим:
dt-  , откуда
, откуда 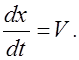 (2.2.9)
(2.2.9)
Из (2.2.9) следует, что фазовая скорость волны (2.2.7) положительна. Таким образом, уравнение (2.2.7) описывает волну, распространяющуюся в положительном направлении оси X.Очевидно, уравнение волны, распространяющейся в противоположном направлении, можно получить, заменив в уравнении (2.2.7) X на -X, то есть
x=A×cosw(t+ 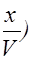 . (2.2.10)
. (2.2.10)
Действительно, приравняв константе фазу волны (2.2.10) и продифференцировав, получим 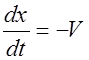 .
.
Уравнению плоской волны можно придать симметричный относительно t и x вид. Для этого введем волновое число k:
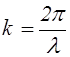 . (2.2.11)
. (2.2.11)
С учетом формулы (2.2.4) из (2.2.11) получаем соотношение
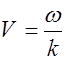 , (2.2.12)
, (2.2.12)
где 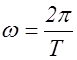 - циклическая частота.
- циклическая частота.
Заменив в уравнении (2.2.7) V согласно (2.2.12) и внеся в скобки w, получим уравнение плоской волны в виде
x=A×cos(wt-kx) . (2.2.13)
Очевидно, уравнение (2.2.10) также может быть записано в симметричном относительно t и x виде и будет отличаться от (2.2.13) знаком в аргументе у косинуса.
Получим теперь уравнение сферической волны. Если рассматривать волну на расстояниях от источника, значительно превышающих его размеры, то источник можно считать точечным. Такой источник в случае, когда скорость распространения волны во всех направлениях одна и та же, создает сферические волны. Пусть фаза колебаний источника равна wt , тогда фаза колебаний частиц среды лежащих на волновой поверхности радиуса r будет равна 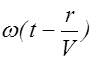 . В этом выражении учтено, что расстояние r волна проходит за время
. В этом выражении учтено, что расстояние r волна проходит за время 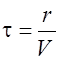 .
.
Как будет показано в §2.4,амплитуда колебаний в сферической волне убывает по закону 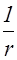 , даже если среда не поглощает энергию волны. Следовательно, уравнение сферической волны имеет вид:
, даже если среда не поглощает энергию волны. Следовательно, уравнение сферической волны имеет вид:
x= 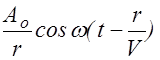 , (2.2.14)
, (2.2.14)
где константа A0 - численно равна амплитуде колебаний на расстоянии, равном единице длины. Размерность ее равна размерности амплитуды (зависит от физической природы волнового процесса), умноженной на размерность длины.
Получим уравнение плоской волны, распространяющейся в произвольном направлении, образующем с осями координат x, y,  z углы a, b и g.
z углы a, b и g.
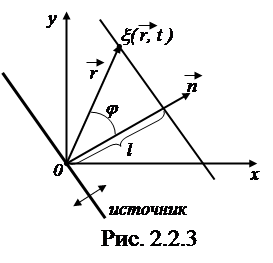 Пусть источником колебаний будет плоская пластина, проходящая через начало координат (рис.2.2.3), колебания которой описываются уравнением
Пусть источником колебаний будет плоская пластина, проходящая через начало координат (рис.2.2.3), колебания которой описываются уравнением
x(0,t) = Acoswt. (2.2.15)
В плоскости, отстоящей от начала координат на расстоянии l, колебания частиц будут отставать от колебаний источника на время t 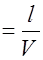
 и, следовательно, их смещение будет описываться уравнением
и, следовательно, их смещение будет описываться уравнением
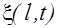 =
= 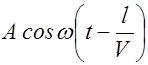 . (2.2.16)
. (2.2.16)
Выразим l через радиус-вектор 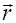 точек рассматриваемой плоскости (это плоскость является волновой поверхностью).
точек рассматриваемой плоскости (это плоскость является волновой поверхностью).
Для этого введем единичный вектор 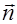 нормали к волновой поверхности. Из рис.2.2.3 следует, что
нормали к волновой поверхности. Из рис.2.2.3 следует, что
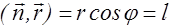 . (2.2.17)
. (2.2.17)
Подставим выражение (2.2.17) в уравнение (2.2.16), тогда получим
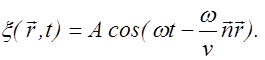 (2.2.18)
(2.2.18)
Учтем, что 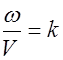 и введем вектор
и введем вектор
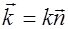 , (2.2.19)
, (2.2.19)
Дата добавления: 2015-07-22; просмотров: 2755;
