Свойства сетей Петри
Позиция p  P сети Петри N = (P,Т,I,O) c начальной маркировкой m является k-ограниченной, если m’(p)
P сети Петри N = (P,Т,I,O) c начальной маркировкой m является k-ограниченной, если m’(p)  k для любой достижимой маркировки m’
k для любой достижимой маркировки m’  R(N,m). Позиция называется ограниченной, если она является k-ограниченной для некоторого целого значения k. Сеть Петри ограниченна, если все ее позиции ограниченны.
R(N,m). Позиция называется ограниченной, если она является k-ограниченной для некоторого целого значения k. Сеть Петри ограниченна, если все ее позиции ограниченны.
Позиция p  P сети Петри N = (P,Т,I,O) c начальной маркировкой m является безопасной, если она является 1-ограниченной. Сеть Петрибезопасна, если безопасны все позиции сети.
P сети Петри N = (P,Т,I,O) c начальной маркировкой m является безопасной, если она является 1-ограниченной. Сеть Петрибезопасна, если безопасны все позиции сети.
Сеть Петри N = (P,Т,I,O) с начальной маркировкой m является сохраняющей, если для любой достижимой маркировки m’  R(N,m) справедливо следующее равенство:
R(N,m) справедливо следующее равенство:
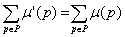 .
.
Тупик в сети Петри – один или множество переходов, которые не могут быть запущены. Определим для сети Петри N с начальной маркировкойm следующие уровни активности переходов:
Уровень 0: Переход t обладает активностью уровня 0 и называется мёртвым, если он никогда не может быть запущен.
Уровень 1: Переход t обладает активностью уровня 1 и называется потенциально живым, если существует такаяm’  R(N,m), что t разрешён вm’.
R(N,m), что t разрешён вm’.
Уровень 2: Переход t, обладает активностью уровня 2 и называется живым, если для всякой m’  R(N,m) переход t является потенциально живым для сети Петри N с начальной маркировкой m’.
R(N,m) переход t является потенциально живым для сети Петри N с начальной маркировкой m’.
Сеть Петри называется живой, если все её переходы являются живыми.
Задача достижимости: Для данной сети Петри с маркировкойm и маркировки m’ определить: m’  R(N,m)?
R(N,m)?
Задача покрываемости:Для данной сети Петри N с начальной маркировкой m и маркировки m’ определить, существует ли такая достижимая маркировка m”  R(N,m), что m" ³ m’.
R(N,m), что m" ³ m’.
(Отношение m" ³ m’ истинно, если каждый элемент маркировки m" не меньше соответствующего элемента маркировки m’.)
Сети Петри присуще некоторое поведение, которое определяется множеством ее возможных последовательностей запусков переходов или ее множеством достижимых маркировок. Понятие эквивалентности сетей Петри определяется через равенство множеств достижимых маркировок.
Сеть Петри N = (P,Т,I,O) с начальной маркировкой m и сеть Петри N’ = (P’,Т’,I’,O’) с начальной маркировкой m’ эквивалентны, если справедливо R(N,m) = R(N’,m’).
Понятие эквивалентности сетей Петри может быть определено также через равенство множеств возможных последовательностей запусков переходов.
Более слабым, по сравнению с эквивалентностью, является свойство включения, определение которого совпадает с определением эквивалентности, с точностью до замены = на 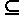 .
.
Дата добавления: 2015-07-18; просмотров: 1179;
