Условия работы подшипника качения, влияющие на его работоспособность

Распределение нагрузки между телами качения. По условию равновесия (рис. 5.18),

F_r=F₀+2F₁cosγ+2F2cos2γ+...+2Fncosnγ, (5.16)

где γ=60°/z; z — число шариков.

В уравнение (5.16) входят только те члены, для которых угол nγ меньше 90°, так как верхняя половина подшипника не нагружена.

Исследование зависимости между силами F₀, F₁, F₂,...F_n с учетом контактных деформаций при условии абсолютной точности размеров шариков и колец и отсутствии радиального зазора позволило установить

F₁=F₀cos^3/2γ, F_n=F₀cos^3/2nγ.

Формула для определения F₀

F₀=F_r/(1+2соs^5/2γ+2соs^5/22γ+...+2cos^5/2/nγ). (5.17)

Подсчитано, что отношение z/(l+2cos^5/2γ+2cos^5/22γ+...+2cos^5/2nγ)≈4,37 для любого числа шариков, встречающегося в подшипнике. При этом

F₀=4,37Fr/z.

Вводя поправку на влияние радиального зазора и неточности размеров деталей, практически принимают

F₀=5F_r/z, F_n=(5F_rcos^3/2nγ)/z. (5.18)

Распределение нагрузки зависит от размера зазора в подшипнике и точности геометрической формы его деталей. Зазоры увеличиваются от износа подшипника в эксплуатации. При этом прогрессивно ухудшаются условия работы вплоть до разрушения подшипника.

Кинематика подшипника. Шарик в подшипнике совершает планетарное движение. На рис. 5.19 изображен план скоростей для случая вращения внутреннего кольца. Здесь

v₁=ωD₁/2; v₀=v_l/2.

Угловая скорость шарика вокруг своей оси

ω_ш=2(v₁-v₂)/D_w=0,5ωD₁/D_w. (5.21)

Угловая скорость шарика вокруг оси вала, или угловая скорость сепаратора,

ω_c=2v₀/D_m=0,5ωD₁/(D₁+D_w)≈0,5ω. (5.22)

Сепаратор вращается вместе с валом с угловой скоростью, равной примерно половине угловой скорости вала. Угловая скорость сепаратора зависит от размеров шарика. Чем больше D_w при постоянном D₁, тем меньше ω_c. Контакт шарика с кольцами осуществляется по некоторой дуге aba (рис.5.19). Скорости точек а и b при качении шарика различны. Если допустить, что в точке b нет скольжения, то оно будет в точке а. В шариковых подшипниках наряду с трением качения присутствует трение скольжения, которое создает дополнительный износ и потери в шариковых подшипниках. В роликовых подшипниках наблюдается чистое качение. Потери и износ в роликовых подшипниках меньшие, чем в шариковых.

Динамика подшипника. Каждый шарик или ролик подшипника (рис. 5.21, а) прижат к наружному кольцу центробежной силой

F_цб=m 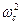D_m/2, (5.23)

где т—масса шарика или ролика.

У высокоскоростных подшипников влияние центробежных сил возрастает. Центробежные силы особенно неблагоприятны для упорных подшипников (рис. 5.20,б). Здесь они расклинивают кольца и повышают трение и износ.

Кроме центробежных сил на шарики упорного подшипника действует гироскопический момент, связанный с изменением направления оси вращения шарика в пространстве (рис. 5.20,б):

М_г=Jω_шω_с, (5.24)

где J—момент инерции шарика относительно своей оси. Под действием гироскопического момента шарик стремится повернуться в направлении, перпендикулярном направлению качения. Вращение возможно, если

М_г>М_т=FfD_w, (5.25)

где М_т—момент сил трения между шариком и кольцами; F—нагрузка на шарик. Вращение шариков под действием М_Т сопровождается дополнительными потерями и износом. В радиальных подшипниках не действуют гироскопические моменты. Радиально-упорные подшипники занимают промежуточное положение. Для них

М_г=Jω_шω_сsinα, (5.26)

где α—угол давления.

Вредное влияние динамических факторов больше всего проявляется в упорных подшипниках. При высоких частотах вращения упорные подшипники рекомендуют заменять упорно-радиальными.