Эквивалентная статическая нагрузка

P₀=X₀F_r+Y₀F_a, но не меньше чем P₀=F_r, 5.34

где F_r и F_a — радиальная и осевая силы; Х₀ и Y₀ — коэффициенты радиальной и осевой статических сил. P₀=F_a для упорных подшипников. Например:

1) Х₀=0,6 и Y₀=0,5—радиальные шарикоподшипники однорядные и двухрядные;

2) Х₀=0,5 и Y₀=0,47...0,28 (при α=12...36° соответственно)—радиально-упорные шарикоподшипники;

3) Х₀=0,5 и Y₀=0,22ctgα—конические и самоустанавливающиеся шарико и роликоподшипники.

Предельная быстроходность подшипника ограничивается указанной в каталоге предельной частотой вращения n_пр. Это наибольшая частота вращения, за пределами которой расчетная долговечность не гарантируется. Для оценки предельной быстроходности принят условный скоростной параметр

[D_mn]=const,

где D_m—диаметр окружности центров тел качения, мм; п — частота вращения, мин^-1.

Допускаемое значение [D_mn] зависит от конструктивных и эксплуатационных параметров: тип подшипника, типа сепаратора, класса точности, типа смазки и др.

Например, подшипник шариковый радиальный однорядный со стальным штампованным сепаратором классов точности 0 и 6 [D_mn]=5,5·10⁵ при жидкой и 4,5·10⁵ при пластичной смазках; шариковый упорный однорядный и при тех же параметрах [D_mn]=1,8·10⁵ и 1,3·10⁵.

При известном [D_mn] определяют n_пр для каждого типоразмера подшипника, который указан в каталогах.

Особенности расчета нагрузки радиально-упорных подшипников связаны с наклоном контактных линий на угол α к торцовой плоскости подшипника (рис.5.13 и 5.18). На рис.5.21 в качестве примера изображены конструктивная а и расчетная б схемы для подшипников вала конической шестерни. Нагрузки в зацеплении приведены к оси вала: 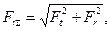, M=F_ad_m1/2, где F_t, F_r и F_a- усилия действующие в зацеплении.

Нагрузка на конец вала —F_M. Радиальные нагрузки подшипников F_rl и F_r2 определяют обычным способом по двум уравнениям равновесия: ΣY=0 и ΣM=0.

F_rl и F_r2 приложены в точках пересечения контактных нормалей с осью вала. Расстояние между этими точками зависит от схемы расположения подшипников и значения угла α. Если каждый подшипник на рис. 5.21 развернуть в плоскости чертежа на 180° с соответствующим изменением положения упорных буртиков, то точки приложения сил F_rl и F_r2 сместятся внутрь, расстояние между ними уменьшится, а силы F_rl и F_r2 возрастут — неблагоприятный вариант.

Для определения двух осевых нагрузок F_al и F_a2 имеем только одно уравнение ΣX=0, или

F_a-F_a1+F_a2=0. (5.35)

В общем случае F_al не равна F_a2, Наклон контактных линий в радиально-упорных подшипниках приводит к тому, что радиальные нагрузки F, сопровождаются внутренними осевыми силами S, которые стремятся раздвинуть кольца подшипника в осевом направлении (рис.5.21,в). Этому препятствуют реакции F_al и F_a2. Очевидно, должно быть

F_a1≥S₁ и F_a2≥S₂, (5.36)

иначе кольца раздвинутся.

Осевая сила равна минимально возможной по условию не раздвигания колец, т.е. F_a1=S₁. Так как неизвестно, в каком из подшипников соблюдается это условие, задачу решаем методом попыток. Например, при F_al=S₁ получим

F_a2=S₁-F_a, (5.37)

и если при этом F_a2≥S₂, то осевые силы определены правильно. Если F_a2<S₂, то принимают F_a2=S₂ и находят

F_al=S₂+F_a. (5.38)

При этом обязательно выполняется условие F_al≥S₁ так как при F_al=S₁ было F_a2<S₂, а при увеличении F_a2 должна увеличиваться и F_al.

Значение сил S зависит от типа подшипника, угла ос и условий сборки или регулировки подшипников. Если подшипники собраны с большим зазором, то всю нагрузку воспринимает только один или два ролика. При этом (рис. 5.21,в) S_i=F_ritgα, где i—в общем случае номер опоры.

Зазоры приводят к разрушению подшипников. Зазоры устанавливают, близкие к нулю. При этом под нагрузкой находится примерно половина тел качения, а суммарная осевая составляющая

S_i=eF_ri для радиально-упорных шариковых,

S_i=0,83eF_ri для конических роликоподшипников, (5.39)

где е—параметр осевой нагрузки (см. табл. 5.6)