Полиномы кодовых слов циклического кода делятся без остатка на свой порождающий полином g(x).
Выбор g(x) для построения циклического кода длины n.
Любой полином, который является делителем полинома (xn+1) можно использовать в качестве порождающего. С ростом n число возможных циклических кодов растет. На практике при построении циклических кодов пользуются таблицами разложения полиномов (xn+1) на неприводимые полиномы. Любой неприводимый полином, входящий в разложение, или произведение нескольких неприводимых полиномов можно выбрать в качестве порождающего полинома, который дает соответствующий циклический код.
Пример.
Требуется определить, какие циклические коды можно построить при длине кодового слова n=7.
x7+1=(x+1)(x3+x2+1)(x3+x+1)
Можно построить следующие ЦК:
1. (7,6) с g(x)=x+1
2. (7,1) с g(x)= (x3+x2+1)(x3+x+1)=x6+x4+x3+x5+x3+x2+x3+x+1=
=x6+x5+x4+x3+x2+x+1
3. (7,4) c g(x)= x3+x2+1
4. (7,4) c g(x)= x3+x+1
5. (7,3) c g(x)= (x+1)(x3+x2+1)=x4+x3+x+x3+x2+1=x4+x2+x+1
6. (7,3) c g(x)= (x+1)(x3+x+1)=x4+x2+x+x3+x+1=x4+ x3+x2+1
Процедура кодирования циклическим кодом
Процедура кодирования записывается следующим образом:
V(x)=U(x)*xn-k+R(x)
R(x)= U(x)*xn-k mod g(x)
В этом случае первые k разрядов кодового слова являются информационными, а последние r=n-k - проверочными.
Пример
Закодировать информационную последовательность U=0110 циклическим кодом (7,4) с порождающим полиномом g(x)= x3+x+1.
U(x)= x2+x, r=n-k=3, U(x)*x3= x5+x4
 |
R(x)=( x5+x4) mod (x3+x+1)
R(x)=1
V=0110001 ® V(x)= x5+x4+1
Сложение коэффициентов при одинаковых степенях осуществляется по модулю 2.
Деление можно выполнять в двоичном виде.
U(x)*x3= x5+x4 ® 0110000
g(x) ® 1011
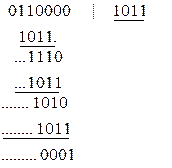
R=001®V=0110001
Дата добавления: 2015-08-26; просмотров: 1205;
