Код Хэмминга. Код Хэмминга предназначен для исправления одиночных ошибок и имеет кодовое расстояние dmin=3

Код Хэмминга предназначен для исправления одиночных ошибок и имеет кодовое расстояние d_min=3. Значения n и k кодов Хэмминга связаны соотношением 2^n-k-1=n . Строки проверочной матрицы Н представляют собой различные ненулевые последовательности длины (n-k). Изначально правила формирования проверочных элементов выбирались (50-е годы) так, чтобы результат контрольных сумм при приеме указывал порядковый номер искаженного элемента.

Пусть a_i – информационные символы, b_i – проверочные символы. Если проверочные символы разместить в кодовой комбинации на позициях, номера которых являются степенью двойки (1, 2, 4, 8 и т.д.), то получаемый синдром в двоичном виде указывает на номер искаженного элемента. Рассмотрим это на примере кода (7,4).

Правило формирования проверочных символов заключается в следующем: значение любого информационного символа должно быть равно сумме по модулю 2 тех проверочных символов, порядковые номера которых входят в разложение по степеням двойки порядкового номера данного информационного символа.

b₁ b₂ a₃ b₄ a₅ a₆ a₇

Решим эту систему уравнений относительно b₁, b₂ и b₄.

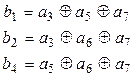
Тогда элементы синдрома S=(s₂,s₁,s₀) равны

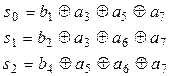
Например, если ошибка произошла в символе a₃ , синдром будет иметь следующий вид S=(011), что означает десятичное число 3.

№7