Код Хэмминга

В качестве примера (n, k)-кода, при задании которого используется матричное представление, рассмотрим код Хэмминга – код с кодовым расстоянием d = 3, позволяющий исправлять все одиночные ошибки. Для кода Хэмминга число разрешённых кодовых комбинаций равно верхней границе – 2ⁿ/(n+ 1). Первые k разрядов кодовых комбинация используются в качестве информационных, их число равно:

.

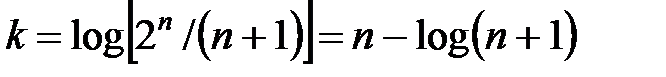Данное уравнение имеет целочисленные решения k = 0, 1, 4, 11, 26, …, которые и определяют соответствующие коды Хэмминга: (3, 1), (7, 4), (15,11) и т.д. Рассмотрим построение (7, 4)-кода. Для этого воспользуемся каноническим представлением порождающей матрицы. Одним из свойств порождающей матрицы является то, что для различных кодовых комбинаций, составленных из информационных разрядов, должны быть различными и проверочные разряды. Так как все вектор-строки единичной подматрицы матрицы G_n,k различны, то и подматрица проверочных разрядов должна состоять из различных ненулевых строк (общее число ненулевых строк должно быть равно 2^r–1).

Вычтем из возможного числа ненулевых строк r строк, образующих единичную матрицу 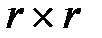, которую следует добавить к транспонированной подматрице проверочных разрядов при определении проверочной матрицы. Тогда останется 2^r–1–r r-разрядных строк с числом единиц не меньше двух. Для кода Хэмминга это число как раз равно числу информационных разрядов. Для (n, k)-кода число различных r-разрядных строк с числом единиц не меньше двух равно числу строк в порождающей матрице. Это свойство позволяет составить непосредственно один из вариантов порождающей матрицы (7, 4)-кода, например, такой:

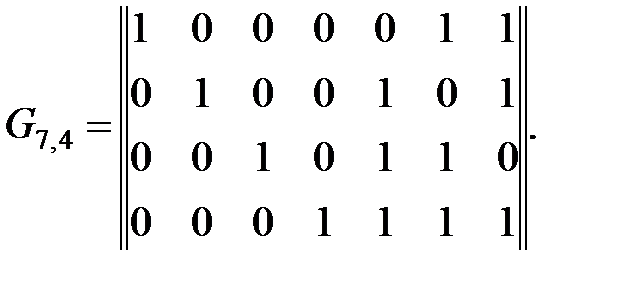
Учитывая связь элементов порождающей и проверочной матриц, представленных в канонической форме, имеем:

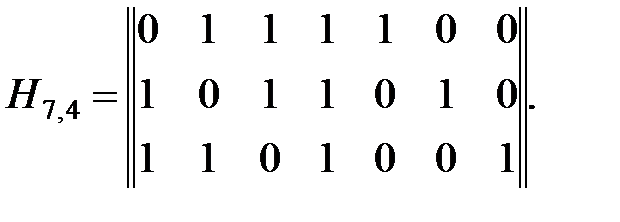
Проверим способность разработанного (7, 4) кода исправлять одиночные ошибки. Пусть передаваемая кодовая комбинация v (7, 4)-кода образована путём сложения первой, второй и четвёртой строк матрицы G_7,4, тогда v = 1101001.

Предположим, что при передаче по каналу произошла ошибка в третьем разряде кодовой комбинации v. В этом случае на приёмной стороне канала будет получена кодовая комбинация v' = 1111001. Умножим принятую кодовую комбинацию на транспонированную проверочную матрицу H_7,4:

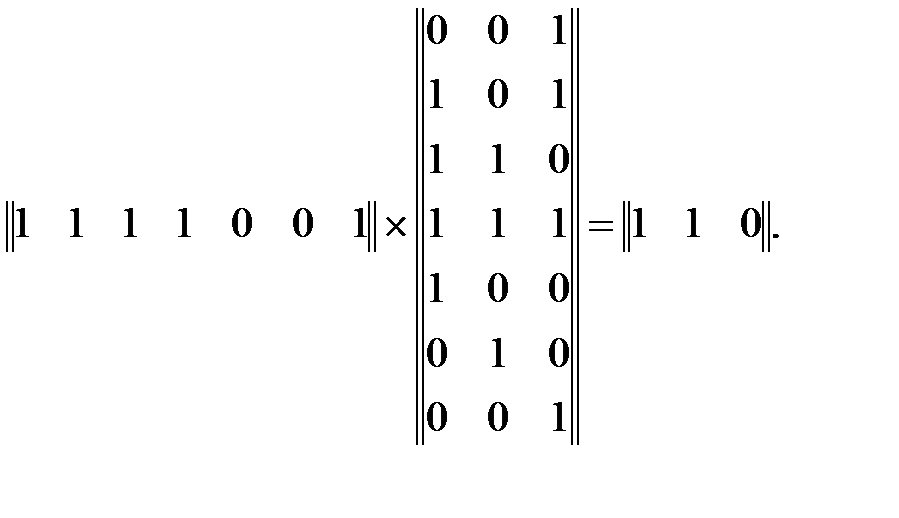
Отличие от нуля синдрома говорит о том, что произошла ошибка. Чтобы определить, в каком разряде кодовой комбинации произошла ошибка, проверим, с какой строкой матрицы транспонированной матрицы H_7,4 совпадает синдром. Как видно, он совпадает с третьей строкой. Следовательно, ошибка произошла в третьем разряде кодовой комбинации. В декодирующих устройствах систем передачи информации результат перемножения принятой кодовой комбинации на проверочную матрицу (синдром ошибки) используется для автоматического исправления соответствующего разряда.