Теоремы Кантора-Бернштейна

1. Если A Í B Í C, причем A ~ C, то A ~ B.

2. Если A эквивалентно подмножеству множества B, а B эквивалентно подмножеству множества A, то A ~ B.

(Без доказательства).

Основные свойства отображений можно сформулировать в виде следующих теорем.

Теорема 1.1. f ^–1 (A È B) = f ^–1 (A) È f ^–1 (B) – прообраз объединения двух множеств равен объединению их прообразов.

Доказательство. Пусть xÎf ^–1 (A) È f ^–1 (B). Тогда или xÎf ^–1 (A) или хÎf ^–1 (B). В первом случае y = f(x)ÎА, во втором yÎВ. В любом случае yÎА È В, поэтому xÎf ^–1 (A È B).

Докажем обратное включение. Пусть xÎf ^–1 (A È B), тогда y = f(x) Î A È B. Значит или yÎА, или yÎВ. Если yÎА, то f ^–1 (y) Í f ^–1 (A). Так как xÎf ^–1 (y), то отсюда следует, что xÎf ^–1 (A). Если же yÎВ, то f ^–1 (y) Í f ^–1 (B), что влечет xÎf ^–1 (В). В любом случае xÎf ^–1 (A) È f ^–1 (B). Поэтому, если xÎf ^–1 (A È B), то xÎf ^–1 (A) È f ^–1 (B), что и требовалось доказать.

Теорема 1.2. f ^–1 (A Ç B) = f ^–1 (A) Ç f ^–1 (B) – прообраз пересечения двух множеств равен пересечению их прообразов.

Доказательство. Пусть xÎf ^–1 (A Ç B), тогда y = f(x)ÎA Ç B. Значит, yÎА и yÎВ. Если yÎА, то f ^–1 (y) Í f ^–1 (A), а если yÎВ, то f ^–1 (y) Í f ^–1 (B). Эти включения должны выполняться одновременно, следовательно, f ^–1 (y) Í f ^–1 (A) Ç f ^–1 (B), а значит, хÎf ^–1 (A) Ç f ^–1 (B). Таким образом, f ^–1 (A Ç B) Í f ^–1 (A) Ç f ^–1 (B).

Докажем обратное включение. Пусть xÎf ^–1(A) Ç f ^–1(B), тогда xÎ f ^–1(A) и xÎf ^–1(B). Если xÎf ^–1(A), то y = f(x)ÎA. Если же xÎf ^–1(B), то y = f(x)ÎB. Так как yÎA и yÎB, то yÎAÇB и поэтому f ^–1(y) Í f ^–1(A Ç B). Значит, хÎf ^–1(A Ç B) и отсюда следует, что f ^–1(A) Ç f ^–1(B) Í f ^–1(A Ç B).

Эти два включения означают, что f ^–1(AÇB) = f ^–1(A)Çf ^-1(B), что и требовалось доказать.

Теорема 1.3. f (A È B) = f (A) È f (B) – образ объединения двух множеств равен объединению их образов.

Доказательство. Пусть yÎf(A È B), тогда для любого x из множества f ^–1(y) выполняется принадлежность хÎA È B. Поэтому xÎA или xÎB. В первом случае y = f(x)Îf(A), во втором – y = f(x)Îf(B). Так как yÎf(A) или yÎf(B), то yÎf(A) È f(B) и, следовательно, f(A È B) Í f(A) È f(B).

Докажем обратное включение. Пусть yÎf(A) È f(B), тогда yÎf(A) и f ^–1(y) Í A или yÎf(B) и f ^–1(y) Í B. Соответственно получаем, что xÎA или xÎB, т.е. xÎA È B и тогда y = f(x)Îf(A È B). Доказано включение f(A) È f(B) Í f(A È B). Следовательно, f(A È B) = f(A) È f(B). что и требовалось доказать.

Замечание. Образ пересечения двух множеств не обязательно совпадает с пересечением их образов. Рассмотрим пример.

Пусть A и B – множества точек на плоскости:

A = { (x, y) | 0 £ x £ 1, y = 2 },

B = { (x, y) | 0 £ x £ 1, y = 1 }.

С помощью проектирования точек на ось ОХ построим отображение А и В на множество С = { (x, y) | 0 £ x £ 1, y = 0 }. Так как f(A) = C, f(B) = C, то f(A) Ç f(B) = C. Но множества A и B не пересекаются и f(A Ç B) = f(Æ) = Æ, т.е. мы показали, что f(A Ç B) ¹ f(A) Ç f(B).

Теоремы 1, 2, 3 остаются в силе при любом конечном и бесконечном числе множеств. Например, теорема 1.1 примет вид:

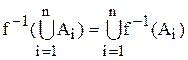. (1)

где A₁, A₂, . . . – некоторая система множеств.

Докажем (1) с помощью метода математической индукции.

1. При n = 2 равенство f ^–1(A₁ È A₂) = f ^–1(A₁) È f ^–1(A₂) справедливо согласно теореме 1.1.

2. Предположим, что равенство верно при любом n £ k.

3. Докажем, что равенство верно при n = k+1. Обозначим B = .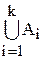

Тогда f ^–1 ) = f ^–1 (B È A_k+1) = f ^–1 (B) È f ^–1 (A_k+1),

так как для двух множеств В и A_k+1 теорема верна. Но по предположению индукции для k множеств теорема также верна, поэтому

f ^–1 (B)= .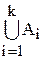

Отсюда следует требуемое равенство.

Тема 2. Мощность множества