Свойства счетных множеств

1. Всякое подмножество счетного множества конечно или счетно.

Доказательство. Пусть А – счетное множество и B Í А. Поскольку А счетно, то занумеруем его элементы и построим из них последовательность

a₁, a₂, a₃, . . .

Из этой последовательности выделим все элементы, принадлежащие множеству B, т.е. рассмотрим подпоследовательность

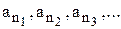
Возможны следующие случаи:

1) Множество B конечно – тогда теорема верна.

2) Множество B бесконечно. Поскольку элементы множества B занумерованы, то в этом случае оно является счетным, что и требовалось доказать.

2. Объединение любого конечного или счетного множества счетных множеств снова является счетным.

Доказательство. Пусть множества А₁, A₂, . . . , А_n, . . . – счетные. Если их число не более, чем счетно, то множества можно занумеровать и расположить принадлежащие им элементы в таблицу

А₁ = {a₁₁, a₁₂, a₁₃, . . .}

А₂ = {a₂₁, a₂₂, a₂₃, . . .}

А₃ = {a₃₁, a₃₂, a₃₃, . . .}

. . . . . . . . . . . . . . . . .

Пусть B = 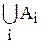. Построим последовательность подобно тому, как это было сделано при доказательстве счетности Q.

b₁ = a₁₁, b₂ = a₁₂, b₃ = a₂₁, b₄ = a₃₁, b₅ = a₂₂, . . . (1)

Если множества А_i попарно пересекаются (А_i ÇА_j ¹ Æ), то в последовательность (1) не включаются те элементы, которые уже занумерованы. Таким образом, построено взаимно однозначное соответствие между множествами B и N. Следовательно, множество B счетно.

3. Всякое бесконечное множество содержит счетное подмножество.

Доказательство. Пусть М – произвольное бесконечное множество. Выберем в нем произвольный первый элемент и обозначим его a₁ , затем – элемент a₂ и т.д. Получаем последовательность a₁, a₂, . . . , которая не может оборваться на каком-то элементе, т.к. М бесконечно. Следовательно, данная последовательность образует счетное подмножество множества М.

Доказанная теорема позволяет утверждать, что среди бесконечных множеств счетное множество является самым "маленьким".

Если множество конечно или счетно то говорят, что оно не более, чем счетно.