Основные свойства операций

1. Коммутативность:

А Ç В = В Ç А; А È В = В È А.

2. Ассоциативность:

(А Ç В) Ç С = А Ç (В Ç С) = А Ç В Ç С;

(А È B) È С = А È (В È С) = А È В È С.

Свойствами коммутативности и ассоциативности обладают многие операции. Чтобы не создалось впечатления, что коммутативность и ассоциативность являются общими свойствами всех операций приведем пример неассоциативной операции – возведение в степень: (2³)² = 8² = 64; 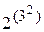= 2⁸ = 512. Некоммутативной операцией является операция умножения матриц (АВ ¹ ВА).

3. Взаимная дистрибутивность:

а) (А È В) Ç С = (А Ç С) È (В Ç С);

б) (А Ç B) È С = (А È С) Ç (В È С).

Для вещественных чисел выполняется свойство дистрибутивности операции умножения относительно сложения a(b + с) = аb + ас. Операции È и Ç множеств – взаимно дистрибутивны:

Докажем равенство а).

Предположим, что xÎ(А È В) Ç С, тогда xÎС и xÎА или xÎВ. Рассмотрим первый случай xÎС и xÎА. Тогда хÎА Ç С, а значит, по определению объединения, хÎ(А Ç С) È (В Ç С). (Можно объединить с любым множеством)

Во втором случае, т.е. при xÎС и xÎВ получаем, что xÎ (В Ç С) È (А Ç С). Таким образом, мы доказали включение

[(А È В) Ç С] Í [(А Ç С) È (В Ç С)].

Докажем обратное включение. Пусть хÎ(А Ç С) È (В Ç С), тогда либо хÎА Ç С либо хÎВ Ç С. В первом случае хÎА и хÎС. Во втором случае хÎВ и xÎС. В обоих случаях получаем, что хÎС и хÎА или хÎВ.Следовательно, хÎ (А È В) Ç С. Тем самым доказано включение (А Ç С) È (В Ç С) Í (А È В) Ç С.

Из этих включений следует, что (А È В) Ç С = (А Ç С) È (ВÇС), что и требовалось доказать.

4. Идемпотентность: A È A = A; A Ç A = A.

5. Законы поглощения: (A Ç B) È A = A; (A È B) Ç A = A.

6. Свойства нуля: A È Æ =A; A Ç Æ = Æ.

7. Свойства единицы: A È U =U; A Ç U = A.

8. Инволютивность: .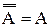

9. Законы де Моргана: ; .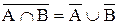

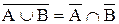10. Свойства дополнения: ; .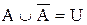

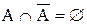Законы де Моргана можно обобщить на произвольное количество множеств. Пусть А₁, А₂, . . . – некоторые множества и пусть все они включены в S (А₁, А₂, . . . Í S). Тогда выполняются следующие соотношения.

11. 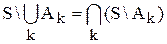– дополнение объединения множеств равно пересечению их дополнений.

12. 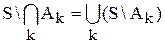– дополнение пересечения множеств равно объединению их дополнений.

Докажем свойство 11. Пусть хÎ 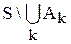, тогда хÏ 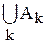, значит, x не принадлежит ни одному из множеств A_k ("k, хÏА_k). Следовательно, по определению дополнения, хÎS\А_k для любого k. Отсюда вытекает, что хÎ .

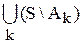Обратно, пусть хÎ 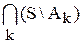. Тогда этот элемент принадлежит каждому из множеств S \ A_k ("k, хÎS \ A_k). Следовательно, хÏA_k для любого k, а, значит, хÏ 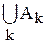и поэтому хÎ 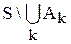, что и требовалось доказать.