Представление множеств в ЭВМ

Понятие “представление в ЭВМ” означает описание в терминах используемой системы программирования структуры данных, применяемой для хранения информации об объекте и алгоритмов, реализующих присущие данному объекту операций. Таким образом, применительно к множествам определение представления в ЭВМ подразумевает описание способа хранения информации о принадлежности элементов множеству и описание алгоритмов для вычисления объединения, пересечения и других теоретико-множественных операций. Будем предполагать, что в используемой системе программирования доступны такие структуры данных, как массивы, записи и указатели.

1. Операции с подмножествами заданного универсума. Пусть универсум U – конечный, и число его элементов n не превосходит разрядности ЭВМ. Занумеруем эти элементы: U = {u₁, u₂,…, u_n}. Тогда любое подмножество АÍU представляется машинным кодом С, в котором

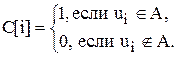
В этом случае код пересечения произвольных множеств А и В получается, как поразрядное логическое произведение (в Паскале – операция and) кода множества А и кода множества В. Код объединения равен логической сумме (or), код дополнения – инверсии (not). При использовании в качестве носителей кодов 32-разрядных ячеек (в Паскале – данные типа Longint) можно успешно работать с унивесумом, содержащим до 32 элементов.

2. Представление упорядоченными списками. Если универсум велик, или бесконечен, а рассматриваемые его подмножества не очень велики, то множества удобнее представлять списками элементов. Элемент представляется записью с двумя полями: информационным и указателем на следующий элемент. Весь список представляется указателем на первый элемент, а набор списков – массивом указателей на первые элементы наборов. Описание алгоритмов, реализующих основные теоретико-множественные операции см. [Новиков, 1.4.4 – 1.4.7].

3. Специальные представления. В некоторых языках программирования предусмотрены данные, аналогичные множествам (в Паскале – тип Set), а также соответствующие операции с ними. Однако, такие операции работают весьма медленно и при больших множествах подобный подход неэффективен.