Операции над множествами. Определим следующие операции.

Определим следующие операции.

1. Объединение. Пусть А и В – произвольные множества. Их объединением называется множество С = А È В, которое состоит из всех элементов, принадлежащих хотя бы одному из множеств А или В.

2. Пересечение. Пересечением множеств А и В называется множество С, состоящее из элементов, одновременно принадлежащих А и В. Обозначается так: C = A Ç B.

3. Разность. Разность множеств А и В – это множество С (С = А \ В), состоящее из элементов множества А, не принадлежащих множеству В. Если В Í А, то разность С = А \ В называется дополнением В до А.

Считается, что все множества включены в некоторое множество U, которое называют универсальным множеством (универсумом). В этом случае дополнение какого-либо множества А до U обозначается С(А) или .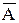

4. Симметричная разность. По определению симметричная разность двух множеств А и В – это множество

С = А D В = (А \ В) È (В \ А).

Перечисленные операции удобно изображать графически с помощью т.н. диаграмм Вена (показать).