Основы алгебры логики.

Алгебра логики – наука, которая занимается логическими функциями, описанием работы и синтезом с их помощью схем различных устройств ЦВМ. Алгебра логики имеет дело с высказываниями. Высказывания могут быть истинными или ложными. Если высказывание истинно, то значение истинности равно 1, если ложно -0. Высказывания могут быть простые и сложные, которые образуются из простых с помощью элементарных логических операций. Простые высказывания обычно называются также логическими переменными, сложные высказывания - логическими функциями.

Основные элементарные логические операции:

1) Логическое отрицание. Обозначается чертой над логической переменной. Например 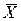читается “не Х”.

Каждая логическая операция характеризуется таблицей истинности, которая показывает значение функции при всех значениях переменных. В данном случае таблица истинности содержит одну переменную, т.е.

Х

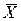
0 1

1 0

Изоб ражение логического элемента “НЕ” на структурной схеме показано на рис. 2.14а.

Рис. 2.14. Изображение основных логических элементов.

а) элемент «НЕ»; б) элемент «ИЛИ»; в) элемент «И»

2) Логическое сложение (дизъюнкция). Обозначается значком V. Например Х₁VХ₂ читается как “Х₁ или Х₂”.Результаты логического сложения истинен (1) коли хотя бы одна из переменных (Х₁ или X₂) истинна (1)

Таблица истинности

Изображение логического элемента “ИЛИ” на структурной схеме показано на рис.2.14 б.

3) Логическое умножение (конъюнкция). Обозначается значком ^. Например Х1^Х2 читается “Х₁ и Х₂”. Результат логического умножения истинен (1), только тогда, когда обе переменных истинны (1)

Таблица истинности

Изображение логического элемента “И” на структурной схеме показано на рис.2.14в:

Основные законы алгебры логики:

1. Переместительный

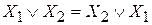
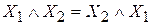
2. Сочетательный

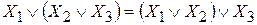
3. Распределительный

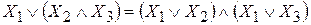
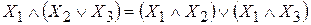
4. Отрицания

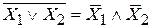
Справедливость любого закона может быть показана с помощью таблицы истинности.

Покажем справедливость последнего закона

Х1	Х2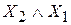

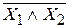
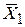
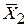
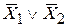
Из таблицы видно, что при всех сочетаниях значений логических переменных Х₁ и Х₂ значения логических функци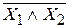й и 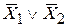совпадают. Следовательно, эти логические функции тождественны, т.е. закон справедлив.