Пример. Число –127
Код модуля числа 0,1111111
Обратный код числа 1,0000000. Представление числа в обратном коде показано на рис. 2.11
Рис. 2.11
3. Дополнительный код получается образованием обратного кода с последующим прибавлением единицы к его младшему разряду.
Пример. Представление числа –1 в дополнительном коде показано на рис. 2.12
Рис. 2.12
Представление числа –127 в дополнительном коде показано на рис. 2.13
Рис. 2.13
Обычно отрицательные десятичные числа при вводе в машину автоматически преобразуются в обратный или дополнительный двоичный код и в таком виде хранятся и участвуют в операциях. При выводе таких чисел из машины происходит обратное преобразование в отрицательные десятичные числа.
Использование различных способов изображения отрицательных чисел в ЦВМ обуславливает целый ряд особенностей выполнения операции алгебраического сложения двоичных чисел.
При сложении обратных кодов чисел Х1 и Х2 имеют место четыре основных и два особых случая.
1. Х1>0 и X2>0. При суммировании складываются все разряды, включая разряд знака.
Пример
Десятичная запись Двоичные коды
| + | |
(5)
+
(9)
(14)
2. Х1>0, X2<0 и |X2|>X1
Пример
Десятичная запись Двоичные коды
| + | |
+
 -10
-10
 -7
-7
При переводе обратного кода (обр) в прямой (пр) получим:
1 1111000обр=1 0000111пр= -710
3. Х1>0, X2<0 и |X2|<X1
Пример
Десятичная запись Двоичные коды
| + | |
 0 0
| |
| +1 | |
+
 -3
-3
Полученный непосредственно сразу неверный результат (число 6) исправляется путем переноса единицы из знакового разряда в младший разряд суммы. При этом получается правильный результат – число 710
4. Х1<0 и X2<0
Пример.
Десятичная запись Двоичные коды
| + | |
 1 1
| |
| +1 | |
 -3
-3
+
 -7
-7
-10

Полученный непосредственно сразу неверный результат (обратный код числа –1110) исправляется путем переноса единицы из знакового разряда в младший разряд суммы. 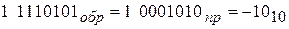
При выполнении операции может появиться число, старшие разряды которого не помещаются в отведенной для него области памяти – возникает переполнение разрядной сетки формата числа. Рассмотрим два возможных случая переполнения.
1. Х1>0 , X2>0 и S=X1+X2  2n-1, где n – количество разрядов формата числа (для однобайтового формата n=8, 2n-1=27=128)
2n-1, где n – количество разрядов формата числа (для однобайтового формата n=8, 2n-1=27=128)
Пример
Десятичная запись Двоичные коды
| + | |
+
97
 162
162
Здесь имеет место переполнение разрядной сетки: семи разрядов цифровой части недостаточно для размещения восьмиразрядной суммы (16210=101000102), поэтому старший разряд суммы оказывается в знаковом разряде и знак суммы оказывается несовпадающим со знаком слагаемых, что является признаком переполнения разрядной сетки.
2 Х1<0, X2<0 и S=|X1|+|X2|  2n-1
2n-1
Пример
Десятичная запись Двоичные коды
| + | |
 0 0
| |
| +1 |
 -63
-63
+
 -95
-95
-158

Здесь также знак суммы не совпадает со знаками слагаемых, что является признаком переполнения разрядной сетки.
При сложении дополнительных кодов чисел Х1 и Х2 имеют место те же четыре основных и два особых случая.
1. Х1>0 и X2>0. Аналогично случаю 1 для обратных кодов.
2. Х1>0, X2<0 и |X2|>X1.
Пример.
Десятичная запись Двоичные коды
| + | |
-
 10
10
 -7
-7
При переводе дополнительного (доп) кода в прямой (пр) получим:
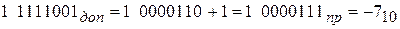
3. Х1>0, X2<0 и |X2|<Х1
Пример
Десятичная запись Двоичные коды
| + | |
 0 0
| |
-
 3
3
 7
7
Единица переноса из знакового разряда отбрасывается.
4. Х1<0, X2<0
Пример
|
| + | |
 1 1
| |
-3
+
|
|

Случаи переполнения разрядной сетки аналогичны случаям переполнения для обратных кодов.
Сравнение использования обратного и дополнительного кодов показывает, что преобразование отрицательного числа в обратный код занимает меньше времени, однако время выполнения сложения в дополнительных кодах меньше, чем в обратных, так как в этом случае отсутствует необходимость переноса единицы из знакового разряда в младший разряд результата.
Дата добавления: 2015-07-14; просмотров: 652;
