Основные формулы, используемые при упрощении логических функций

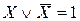
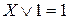
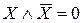
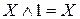
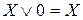
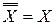
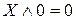
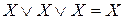
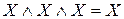
Синтез схемы одноразрядного двоичного сумматора с двумя входами (логического полусумматора).

Составим таблицу работы сумматора в соответствии с двоичной таблицей сложения

Здесь Х₁ и Х₂ – входы (слагаемые), S – сумма, P – перенос в следующий (старший) разряд.

Запишем логические функции S и P из условий их истинности:

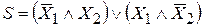
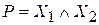
Рис. 2.15. Структурная схема логического полусумматора

Структурная схема логического полусумматора показана на рис. 2.15. Упростим логическую функцию S

Обозначим 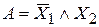, тогда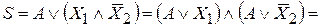

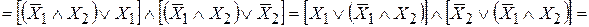
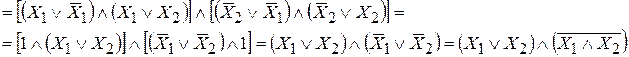
Структурная схема логического полусумматора после упрощения (минимизации) логической функции S, показана на рис.2.16. Эта схема в отличие от предыдущей (рис.2.15) содержит на 2 элемента меньше.

Рис. 2.16. Структурная схема логического полусумматора после

упрощения логической функции S.

На рис. 2.17 показано условное обозначение логического одноразрядного полусумматора.

Рис. 2.17. Условие изображение одноразрядного полусумматора

Схема логического многоразрядного сумматора состоит из ряда одноразрядных сумматоров, у которых, кроме, младшего, имеются 3 входа (2 слагаемых и 1 перенос из предыдущего сумматора). На рис. 2.18 показана схема 4-х разрядного сумматора. Работа сумматора иллюстрируются на примере сложения двоичных чисел Х₁=110 и Х₂=11. при этом S=1001.

Рис. 2.18. Условное изображение 4-х разрядного сумматора