Розв’язання вправ

1. Функція задана формулою f(х) = 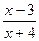. Знайти: 1) f(1); 2) f(0); 3) f(-3); 4) f(t).
2. Для функції на рис.1 указати: а) область визначення; б) область значень; в) координати точок перетину з осями; г) проміжки зростання і спадання функції.

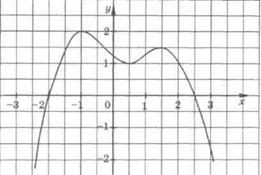Рис. 1

1. Знайти область визначення функції f, які задані формулами:

1) f(х) = х+5;

2) f(х) = х² + 3х – 4;

3) f(х) = ;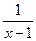

4) f(х) = ;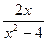

5) f(х) = ;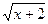

6) f(х) = ;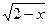

7) f(х) = ;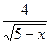

8) f(х) = ;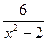

9) f(х) = ;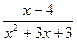

10) f(х) = + ;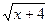

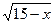11) f(х) = - .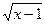

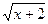1. Знайти область визначення і область значень функцій:

1) f(х) = ;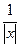

2) f(х) = ;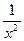

3) f(х) =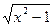

4) f(х) =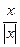

1. З’ясуйте, чи є функція парною або ж непарною:

1) f(х) = 7х⁶;

2) f(х) = 6х⁵ -3х⁷;

3) f(х) = ;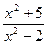

4) f(х) = ;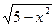

5) f(х) = х² – 2х + 3;

6) f(х) = ;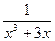

7) f(х) = х .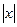

1. На рис.2 зображено графік функції у = f(х) на проміжку 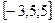. За графіком знайти:

1) 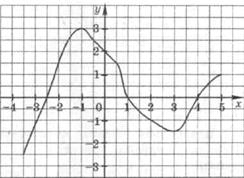f(-2,5); f(-2); f(-0,5); f(0); f(0,5); f(3);

2) значення х, при яких f(х) = -2; f(х) = 3; f(х) = 1,5;

3) нулі функції;

4) найбільше та найменше значення функції;

5) область значень функції;

6) проміжки, на яких функція зростає,

і проміжки, на яких функція спадає;

7) кількість коренів рівняння f(х) = .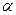

Рис. 2

1. Побудувати графік функції, знайти проміжки, на яких функція зростає, і проміжки, на яких функція спадає:

1) f(х) = 2х -3;

2) f(х) = 4 - 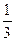х;

3) f(х) = -3х;

4) f(х) = 4;

5) f(х) = ;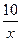

6) f(х) = - ;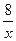

7) f(х) = х² - 2х;

8) f(х) = 4 - х²;

9) f(х) = х² - 6х + 5.

1. Побудувати графік функції, знайти проміжки, на яких функція зростає, і проміжки, на яких функція спадає:

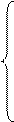
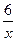, якщо х 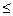-3;

f(х) = 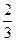х, якщо -3< х < 3;

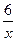, якщо х 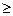3.