Тема. Числові функції, способи їх задання. Основні властивості функції. Обернена і складені функції
План
1. Числові функції.
2. Графік функції.
3. Основні властивості функції.
4. Способи задання функції.
5. Властивості та графіки основних видів функцій.
| 1. Поняття числової функції | |||||||||||
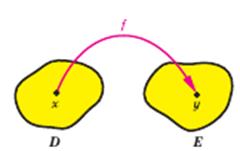
| Числовою функцією з областю визначення D називається залежність, при якій кожному числу х із множини D (області визначення) ставиться у відповідність єдине число у. Записують цю відповідність так: у = f(х). Позначення і терміни D(f) – область визначення Е (f) – область значень х – аргумент (незалежна змінна) у – функція (залежна змінна) f – функція f(х0) – значення функції f у точціх0 | ||||||||||
| 2. Графік функції | |||||||||||
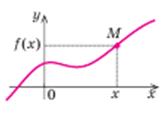
| Графіком функції f називається множина всіх точок координатної площини з координатами (х; f(х)), де перша координата х «пробігає» всю область визначення функції, а друга координата – це відповідне значення функції f у точці х. | ||||||||||
| 3. Основні властивості функції | |||||||||||
| Область визначення функції f – це множина тих значень, яких може набувати аргумент х. Вона позначається D(f). | |||||||||||
| Область значень функції f – це множина, яка складається з усіх чисел f(х), де х належить множині визначення. Її позначають Е (f). | |||||||||||
| Монотонність функції | |||||||||||
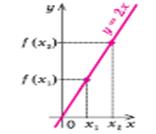
| Функція f(х) зростаюча: якщо х2 > x1, то f(х2) > f(х1) (при збільшенні аргументу відповідні точки графіка піднімаються) | ||||||||||
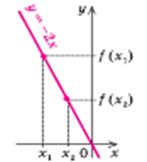
| Функція f(х) спадаюча: якщо х2 > x1, то f(х2) < f(х1) (при збільшенні аргументу відповідні точки графіка опускаються) | ||||||||||
| Парність і непарність функції | |||||||||||
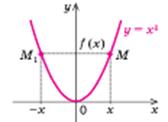
| Функція f(х) парна: f(- х) = f(х) для всіх х з області визначення. Графік парної функції симетричний відносно осі Оу | ||||||||||
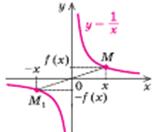
| Функція f(х) непарна: f(- х) = - f(х) для всіх х з області визначення. Графік непарної функції симетричний відносно початку координат - точки О | ||||||||||
| 4. Способи задання функції | |||||||||||
| 1) Аналітичний спосіб | Функція задається за допомогою математичної формули Наприклад, у = х2, у = 5х - 8 | ||||||||||
| 2) табличний спосіб | Функція задається за допомогою таблиці
Наприклад,
| ||||||||||
| 3) Описовий спосіб | Функція задається словесним описом | ||||||||||
| 4) Графічний спосіб | Функція задається за допомогою графіка | ||||||||||
| 5. Властивості та графіки основних видів функцій. | |||||||||||
| 1. Лінійна функція у = kx + b | |||||||||||
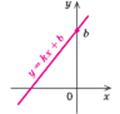 k > 0 k > 0
| Властивості:
1. D(у) = 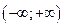 2. Е (у) =
2. Е (у) = 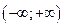 3. Ні парна, ні непарна
4. Зростає: х
3. Ні парна, ні непарна
4. Зростає: х 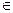 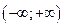
| ||||||||||
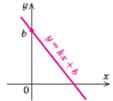 k < 0 k < 0
| Властивості:
1. D(у) = 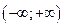 2. Е (у) =
2. Е (у) = 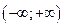 3. Ні парна, ні непарна
4. Спадає: х
3. Ні парна, ні непарна
4. Спадає: х 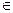 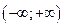
| ||||||||||
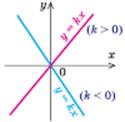
| Властивості:
1. D(у) = 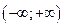 2. Е (у) =
2. Е (у) = 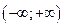 3. Непарна
4. При k > 0 зростає: х
3. Непарна
4. При k > 0 зростає: х 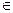 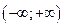 ;
при k < 0 спадає: х ;
при k < 0 спадає: х 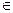 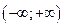
|
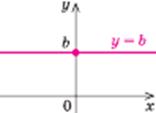
| Властивості:
1. D(у) = 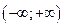 2. Е (у) = b
3. Парна
4. Постійна
2. Е (у) = b
3. Парна
4. Постійна
| |||
2. Обернена пропорційність, функція 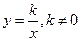
| ||||
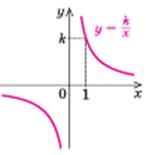 k > 0 k > 0
| Властивості:
1. D(у) = 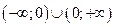 2. Е (у) =
2. Е (у) = 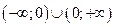 3. Непарна
4. Спадає на кожному з проміжків:
3. Непарна
4. Спадає на кожному з проміжків: 
| |||
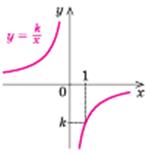 k < 0 k < 0
| Властивості:
1. D(у) = 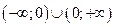 2. Е (у) =
2. Е (у) = 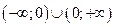 3. Непарна
4. Зростає на кожному з проміжків:
3. Непарна
4. Зростає на кожному з проміжків: 
| |||
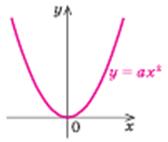
3. Функція у = ах2 ( 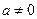 ) )
| ||||
a > 0
| Властивості:
1. D(у) =  2. Е (у) =
2. Е (у) = 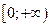 3. Парна
4. Спадає на проміжку
3. Парна
4. Спадає на проміжку 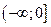 , зростає на проміжку , зростає на проміжку 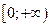
| |||
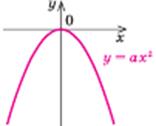
a < 0
| Властивості:
1. D(у) =  2. Е (у) =
2. Е (у) = 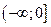 3. Парна
4. Зростає на проміжку
3. Парна
4. Зростає на проміжку 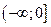 , спадає на проміжку , спадає на проміжку 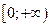
|
4. Квадратична функція у = ax2 + bx + c ( 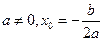 ) )
| ||||
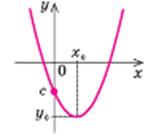
a > 0
| Властивості:
1. D(у) =  2. Е (у) =
2. Е (у) =  3. У загальному випадку - ні парна, ні непарна, при b = 0 функція у = ax2 + c парна
4. Спадає на проміжку
3. У загальному випадку - ні парна, ні непарна, при b = 0 функція у = ax2 + c парна
4. Спадає на проміжку  , зростає на проміжку , зростає на проміжку 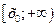
| |||
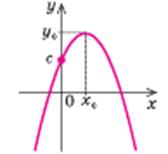
a < 0
| Властивості:
1. D(у) =  2. Е (у) =
2. Е (у) = 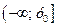 3. У загальному випадку - ні парна, ні непарна, при b = 0 функція у = ax2 + c парна
4. Зростає на проміжку
3. У загальному випадку - ні парна, ні непарна, при b = 0 функція у = ax2 + c парна
4. Зростає на проміжку  , спадає на проміжку , спадає на проміжку 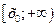
|
Основні варіанти розміщення графіка функції у = ax2 + bx + c ( 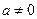 )
)
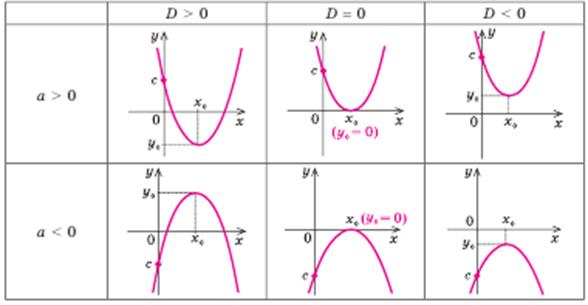 |
Дата добавления: 2015-08-26; просмотров: 2407;