Тема. Ірраціональні рівняння
План
1. Поняття ірраціонального рівняння.
2. Розв’язування ірраціональних рівнянь.
| 1. Поняття ірраціонального рівняння | |
| Означення. Рівняння, у яких змінна міститься під знаком кореня, називають ірраціональним. | |
| 2. Розв’язування ірраціональних рівнянь | |
| 1) За допомогою піднесення обох частин рівняння до одного степеня | |
| При піднесенні обох частин рівняння до непарного степеня отримуємо рівняння, рівносильне заданому (на ОДЗ) | При піднесенні обох частин рівняння до парного степеня можуть з’явитися сторонні корені, які відсіюють перевіркою |
Приклад 1. Розв'язати рівняння 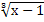 = 2. = 2.
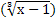 3= 23,
х – 1 = 8,
х = 9.
Відповідь: 9 3= 23,
х – 1 = 8,
х = 9.
Відповідь: 9
| Приклад 2. Розв'язати рівняння 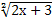 = х. = х.
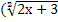 )2= х2,
2х + 3 = х2,
-х2 + 2х + 3 = 0,
х1 = -1, х2 = 3.
Перевірка: )2= х2,
2х + 3 = х2,
-х2 + 2х + 3 = 0,
х1 = -1, х2 = 3.
Перевірка:
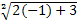 = -1. = -1. 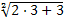 = 3. = 3.
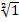 = -1. = -1. 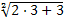 = 3,
1 = 3,
1 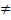 -1 -1 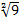 = 3,
3 = 3
Відповідь : 3 = 3,
3 = 3
Відповідь : 3
|
| 2) За допомогою заміни змінних | |
| Якщо в рівнянні змінна входить в одному і тому самому вигляді, то зручно відповідний вираз із змінною позначити однією буквою (новою змінною). | |
Приклад 3. Розв'язати рівняння 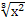 + + 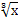 = 2.
Позначимо = 2.
Позначимо 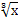 = t.
t 2 + t = 2,
t 2 + t – 2 = 0,
t1 = 1, t2 = -2. = t.
t 2 + t = 2,
t 2 + t – 2 = 0,
t1 = 1, t2 = -2.
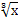 = 1, = 1, 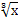 = -2,
х = 1 х = -8
Відповідь: 1;-8. = -2,
х = 1 х = -8
Відповідь: 1;-8.
|
Вправи
1. Розв'язати рівняння
1. 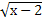 = 1;
2. = 1;
2.  = -3;
3. = -3;
3. 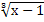 = -3;
4. = -3;
4. 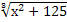 = 5;
5. = 5;
5. 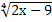 = 3;
6. = 3;
6. 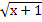 = х – 5;
7. = х – 5;
7. 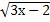 + х = 4;
8. + х = 4;
8. 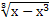 = -х;
9. = -х;
9. 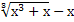 = 0;
10. = 0;
10. 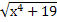 = 10;
11. = 10;
11. 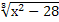 = 2;
12. = 2;
12. 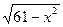 = 5;
13. = 5;
13. 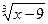 = -3;
14. = -3;
14. 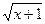 = х – 5;
15. х + = х – 5;
15. х + 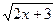 = 6;
16. = 6;
16. 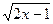 = х – 2;
17. 3 + = х – 2;
17. 3 + 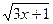 = х;
18. = х;
18. 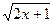 = =  ;
19. ;
19. 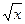 = = 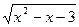 ;
20. 2 + ;
20. 2 +  = = 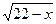 . .
| 1. 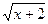 = = 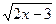 ;
2. ;
2. 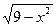 = = 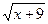 ;
3. х = ;
3. х = 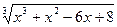 ;
4. х -2 = ;
4. х -2 = 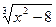 ;
5. х = ;
5. х = 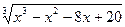 ;
6. х +1 = ;
6. х +1 = 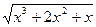 ;
7. ;
7. 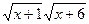 = 6;
8. = 6;
8. 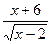 = = 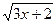 ;
9. ;
9. 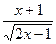 = = 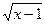 ;
10. ;
10. 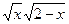 = 2х;
11. = 2х;
11. 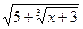 = 3;
12. = 3;
12. 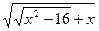 = 2;
13. = 2;
13. 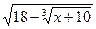 = 4;
14. = 4;
14. 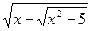 = 1;
15. = 1;
15. 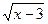 = 1 + = 1 + 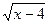 ;
16. ;
16. 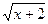 - -  = 2. = 2.
|
Дата добавления: 2015-08-26; просмотров: 977;
