Імовірність. Середні значення фізичних величин. Функція розподілу
Виникнення тих чи інших випадкових подій характеризується їх імовірністю. Імовірність Wi того, що при вимірюванні фізична величина х має певні значення хі, визначається границею відношення числа виникнення певних значень хі до загального числа N всіх вимірювань, при умові, що число таких вимірювань зростає до нескінченності
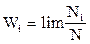 , (2.1.1)
, (2.1.1)
де Ni – число виникнення певних значень хі; N – загальне число всіх вимірювань, серед яких може з’явитись певне, очікуване значення.
Знаючи імовірності виникнення різних результатів вимірювання, можна знайти середнє значення даної фізичної величини. Якщо фізична величина х може мати набір певних значень х1, х2, х3, ... , хі (дискретний спектр), то
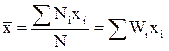 , (2.1.2)
, (2.1.2)
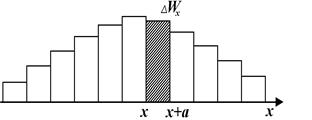
Поділимо систему значень величини х на інтервали однакової ширини а, де а – порівняно мала величина. В цьому випадку будуть одержані інтервали значень величини х, як 0<х<а, а<х<2а, 2а<х<3а, тощо. Нехай імовірність того, що результати вимірювання деякої фізичної величини х виявляться в інтервалі 0<х<а дорівнює ∆W1; в інтервалі а<х<2а – ∆W2; в інтервалі 2а<х<3а – ∆W3, тощо. Побудуємо гістограму одержаних імовірностей ∆W1, ∆W2, ∆W3, ... , ∆Wn вздовж осі значень х (рис. 2.1).
Площа заштрихованої частини на рис. 2.1а відповідає імовірності ∆Wх попадання числа вимірювань величини х в інтервал від х до х+а. Вся площа гістограми відповідає одиниці. Чим менша ширина а, тим точніше визначається розподіл імовірностей вимірювання величини х. У випадку, коли а→0, ступінчата лінія гістограми перетворюється на гладеньку криву, яку називають функцією розподілу імовірностей і позначають f(x) (рис. 2.1 б). В цьому випадку заштрихована смужка відповідає імовірності того, що результати вимірювань виявляться в межах від х до х+dx, тобто
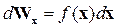 , (2.1.3)
, (2.1.3)
де f(x) – функція розподілу імовірностей вимірювання деякої фізичної величини х в межах значень цієї величини, тобто
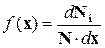 . (2.1.4)
. (2.1.4)
а)

б)
Рис. 2.1 а, б
Площа, обмежена функцією розподілу f(x), подібно до площі гісто-грами, також нормована на одиницю, тобто
 . (2.1.5)
. (2.1.5)
Слід мати на увазі, що величиною х можуть бути будь-які фізичні величини, наприклад, швидкості газових молекул, значення кінетичних енергій молекул, імпульсів молекул, тощо. Тому середнє значення довільної величини х можна отримати, якщо відома її функція розподілу, тобто
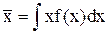 . (2.1.6)
. (2.1.6)
Аналогічно знаходять середнє значення довільної функціональної залежності φ(х), якщо відома функція її розподілу f(x), тобто
 (2.1.7)
(2.1.7) 
Дата добавления: 2015-08-26; просмотров: 1092;
