Розподіл Больцмана. Барометрична формула

Ліву частину рівності (2.2.7) за аналогією з правою частиною запишемо так:

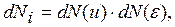(2.2.8)

де dN(u) – число частинок системи, енергія яких є лише потенціальною енергією; dN(e ) – число частинок системи енергія яких є лише кінетичною.

Це дає право поділити рівність (2.2.7) на дві частини, а саме:

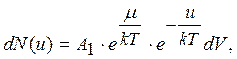(2.2.9)

і

(2.2.10)

У виразі (2.2.9) dN(u) – означає кількість частинок системи, потенціальна енергія яких змінюється в межах від U до U + dU. У виразі (2.2.10) dN(e ) – визначає кількість частинок, кінетична енергія яких змінюється в межах від e до e + de.

Вираз (2.2.9) називають класичним розподілом Больцманачастинок системи за потенціальними енергіями. Вираз (2.2.10) називають класичним розподілом Максвелла частинок за кінетичними енергіями.

Покажемо, що з розподілу Больцмана (2.2.9) легко одержати залежність концентрації частинок в потенціальному полі і барометричну формулу, тобто залежність тиску газової системи від висоти h.

Поділимо ліву і праву частини (2.2.9) на dV, одержимо :

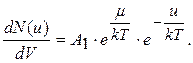
Величина ― концентрація молекул газової системи. У випадку коли U = 0, то n = n₀, тобто

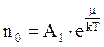
З урахуванням цих позначень розподіл Больцмана матиме вигляд :

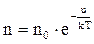. (2.2.11)

З молекулярно-кінетичної теорії відомо, що p = nkT, а тому і p₀ = n₀ kT. Після підстановки n і n₀ з цих формул в (2.2.11) одержимо барометричну формулу, залежність тиску газової системи від висоти у потенціальному полі

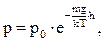(2.2.12)

де p – тиск газу на деякій висоті h; p₀ – тиск газу на рівні, коли h = 0; mgh = U – потенціальна енергія в деякому потенціальному полі.