Алгебраическая форма кватернионов.
Определение. Пусть 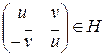 , где
, где 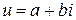 ,
, 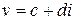 . Тогда
. Тогда 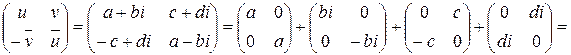
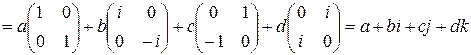 - алгебраическая форма кватерниона, где
- алгебраическая форма кватерниона, где 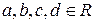 и
и 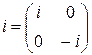 ,
,  ,
, 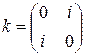 . Таким образом, каждому кватерниону можно поставить в соответствие упорядоченный набор их 4-х элементов:
. Таким образом, каждому кватерниону можно поставить в соответствие упорядоченный набор их 4-х элементов:
Нетрудно заметить следующее:
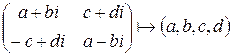 .
.
Более того, если рассматривать тело 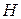 как векторное пространство над полем
как векторное пространство над полем 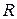 , то каждый кватернион
, то каждый кватернион 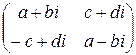 есть вектор с координатами
есть вектор с координатами 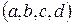 . Тогда следующие кватернионы образуют базис:
. Тогда следующие кватернионы образуют базис:
1=(1,0,0,0) - действительная единица
i=(0,1,0,0)
j=(0,0,1,0)
k=(0,0,1,0).
Определение. Кватернионы i, j, k называются мнимыми кватернионами тела кватернионов.
Замечание. Тело кватернионов не является полем, поскольку не коммутативно, что и подтверждает следующая таблица умножения базисных кватернионов:
| 1\2 | i | j | k | |
| i | j | k | ||
| i | i | -1 | k | -j |
| j | j | -k | -1 | i |
| k | k | j | -i | -1 |
Для того, чтобы перемножить два кватерниона в алгебраической форме, необходимо воспользоваться правилом умножения сумм, учитывая некоммутативность 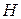 , используя таблицу умножения базисных кватернионов, а затем привести подобные.
, используя таблицу умножения базисных кватернионов, а затем привести подобные.
Определение. Сопряженным к кватерниону 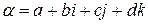 называется кватернион
называется кватернион 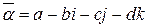 .
.
Следствие. 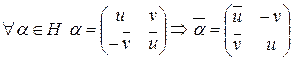 .
.
Определение. Нормой кватерниона 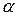 называется
называется 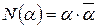 .
.
Следствие 1. 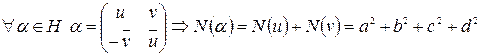 , где
, где 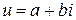 ,
, 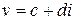 .
.
Следствие 2. Если 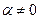 , то
, то 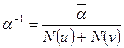 .
.
Дата добавления: 2015-08-21; просмотров: 1200;
