Тело кватернионов.

Открыл Уильям Роуан Гамильтон (ирландец) 1805-1865.

Определение. Ненулевое кольцо с единицей, в котором каждый элемент, отличный от нуля, обратим, называется телом.

Рассмотрим множество матриц:

,

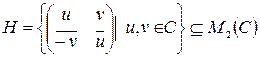где 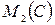- множество квадратных матриц с коэффициентами из поля комплексных чисел.

Теорема 1. 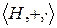тело.

Доказательство.

Покажем, что 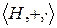- подкольцо кольца 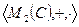, используя признак подкольца:

.

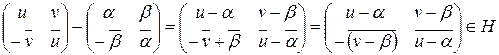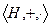- кольцо с единицей (?)

Элемент 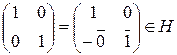является нейтральным элементом по сложению, поскольку .

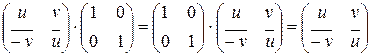Проверим, что любой ненулевой элемент кольца 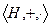обратим:

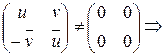
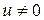или 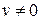. . 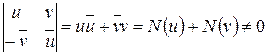Из последнего следует, что любая ненулевая матрица 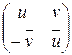невырожденная, следовательно, она обратима в кольце 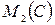. Найдем обратную:

.

что и требовалось доказать.

Определение. Тело 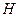назовем телом кватернионов, а его элементы кватернионами.

Теорема 2. Поле комплексных чисел изоморфно вкладывается в тело кватернионов.

Доказательство.

Рассмотрим соответствие , заданное по правилу .

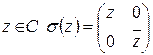Докажем, что 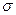- изоморфизм.

- отображение (?)

Всюду определенность очевидна, поскольку для каждого комплексного числа 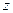можно построить матрицу .

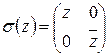Однозначность: (?)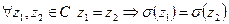

.

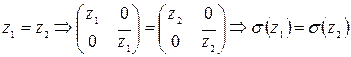- биекция (?)

Инъективность: (?)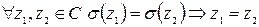

.

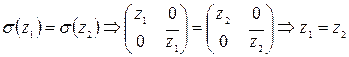Сюръективность: (?)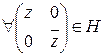

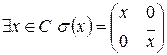Возьмем 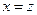, поскольку 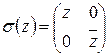. В силу произвольности 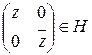сюръективность доказана.

- гомоморфизм (?)

.

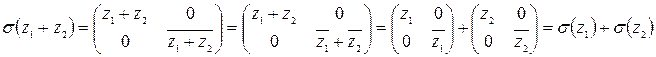
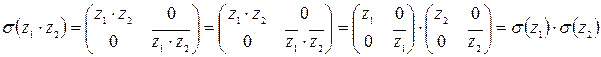что и требовалось доказать.

Замечание. Ввиду изоморфизма, который отмечен в конце доказательства, мы проведем отождествление кватерниона с комплексным числом 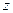. Ввиду этого отождествления получим 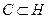(подмножество, более того, подтело).