Доказательство. § - наименьший элемент подмножества;
Возможны случаи:
§ 
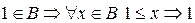- наименьший элемент подмножества;
§ 
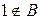. Рассмотрим множество 
. 
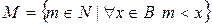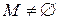, т.к.
. 
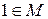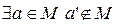. Такой элемент 
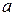обязательно найдется, т.к. в противном случае 
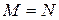. Покажем, что 
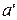наименьший в 
. 
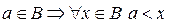. Предположим, что 
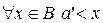. Тогда 
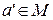. Последнее противоречит условию 
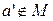, следовательно, предположение неверно. Тогда 
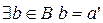такой, что 
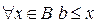. Таким образом, 
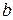- наименьший в .
что и требовалось доказать.
Теорема 8.Любое непустое ограниченное сверху подмножество множества натуральных чисел имеет наибольший элемент.
Дата добавления: 2015-08-21; просмотров: 701;