Цилиндр

На рис. 1 дано построение проекций цилиндра, усеченного фронтально-проецирующей плоскостью γ, наклоненной к оси цилиндра под углом α°.

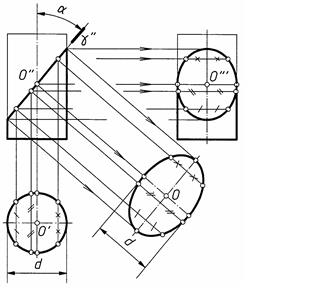
Рис. 1

Плоскость γ пересекает поверхность цилиндра по эллипсу, который проецируется:

- на фронтальную плоскость проекций в отрезок прямой, заключенный между очерковыми образующими и совпадающий с проекцией плоскости γ. Этот отрезок равен действительной длине большой оси эллипса. Центр эллипса (точка О) находится в середине большой оси и на пересечении оси вращения цилиндра с плоскостью эллипса. С точкой О" совпадает фронтальная проекция малой оси эллипса, равная диаметру цилиндра;

- на горизонтальную плоскость проекций – в окружность, так как поверхность цилиндра является проецирующей;

- на профильную плоскость проекций в эллипс, центр которого и большая ось (для заданного положения плоскости γ по отношению к оси цилиндра) построены с помощью горизонтальных линий связи. Малая ось эллипса равна диаметру цилиндра.

На рис. 1 построен истинный вид эллипса на дополнительной плоскости, параллельной плоскости γ.

На рис. 2 даны построения проекций цилиндра со сквозными отверстиями.

Прямоугольное сквозное отверстие на рис. 2, а ограничено двумя вертикальными и двумя горизонтальными плоскостями. Вертикальные боковые плоскости пересекают цилиндр по образующим. Горизонтальные плоскости отверстия пересекают цилиндрическую поверхность по дугам окружностей. На фронтальной и профильной проекциях дуги окружности проецируются в отрезки прямых линий. Горизонтальная проекция дуг совпадает с окружностью, в которую проецируется поверхность цилиндра.

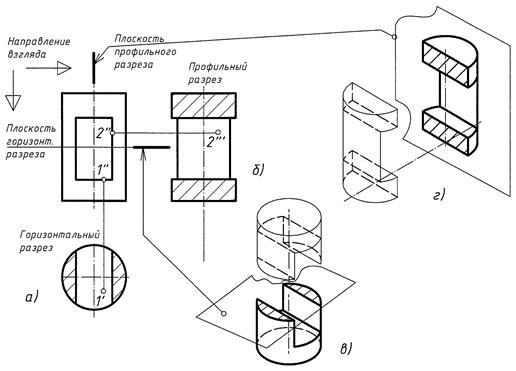Рис. 2

Сквозное отверстие вырезает часть боковой поверхности цилиндра, поэтому очерк фигуры на профильной плоскости проекций изменяется, приобретая вид ломаной линии.

Конус

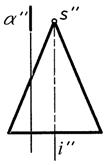
Секущая плоскость не проходит через вершину конуса S (рис. 3)

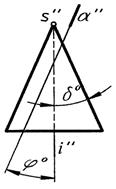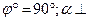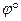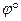i > δB 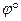= δB < δB 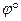= 0; α|| i

окружность эллипс парабола гипербола равносторонняя

гипербола

Рис. 3

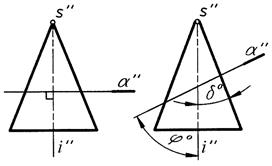
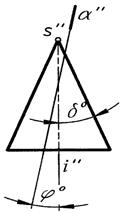
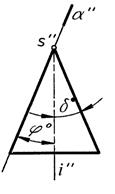
Секущая плоскость проходит через вершину конуса S (рис. 4).

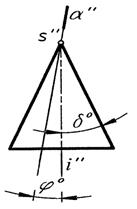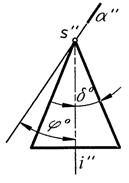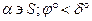
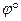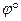= δB > δB

Две прямые (образующие) одна прямая (образующая) точка – вершина S

Рис. 4

На рис. 5 показаны примеры построения пересечения конуса плоскостями

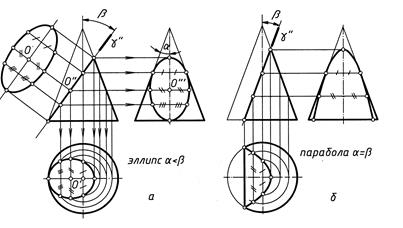
Рис. 5

На рис. 5(а, б) построены проекции двух одинаковых конусов вращения с образующей, наклоненной к оси под углом αB. Конусы усечены фронтально-проецирующими плоскостями γ, не проходящими через вершину и составляющими с осью угол наклона βB. На двух рисунках конуса углы βB имеют разную величину:

– если αB < βB, то в сечении конуса плоскостью γ получится эллипс (рис. 5, а);

– если αB = βB, сечением конуса плоскостью γ будет парабола (рис. 5, б);

Истинный вид эллипса на дополнительной плоскости, параллельной плоскости γ, построен на рис. 5а. На фронтальную плоскость проекции эллипс проецируется в отрезок прямой, заключенный между очерковыми образующими конуса. Центр эллипса О (О', О",О''') находится в середине этого отрезка. С точкой О" совмещается фронтальная проекция малой оси эллипса. Действительная величина малой оси эллипса и другие промежуточные точки, принадлежащие эллипсу, построены с помощью параллелей конуса. Полученные координаты Y точек на горизонтальной плоскости использованы для построения истинного вида эллипса.

Построение проекций конуса со сквозным отверстием показано на рис. 6

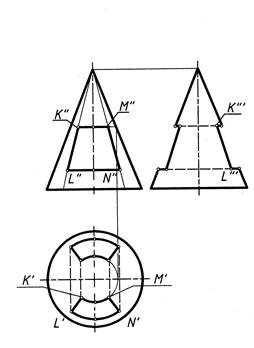
Рис. 6

Сквозное отверстие ограничено по высоте двумя горизонтальными плоскостями, которые пересекают поверхность конуса по двум дугам окружностей между точками К и М и точками L и N. Обозначения присвоены только тем проекциям точек, которые видимы на проекциях фигуры. Две боковые плоскости отверстия проходят через вершину конуса и пересекают его поверхность по образующим. Часть образующих конуса вырезана сквозным отверстием, поэтому очерк конуса на профильной плоскости проекций приобретает вид ломаной линии.

Сфера

На рис. 7 показано построение проекций сферы, усеченной фронтально-проецирующей плоскостью γ, наклоненной к горизонту под углом α°.

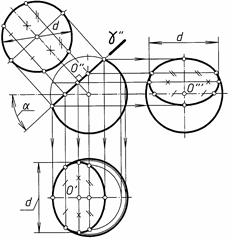
Рис. 7

Плоскость γ рассекает сферу по окружности диаметра d, которая на дополнительную плоскость проекций, параллельную плоскости γ проецируется в натуральную величину.

Фронтальная проекция этой окружности – отрезок прямой, совпадающий с фронтальной проекцией плоскости γ и заключенный между точками пересечения прямой с главным меридианом. Центр окружности – точка О (О', О", О''') – находится в середине отрезка и на пересечении плоскости γ с перпендикуляром, проведенном из центра сферы к плоскости γ.

Горизонтальная проекция окружности – эллипс. Центр эллипса точка О' является горизонтальной проекцией центра окружности диаметра d. Большую ось эллипса находят через горизонтальную проекцию параллели сферы, проходящей через точку О". Вместе с тем большая ось эллипса равна диаметру d окружности, по которой плоскость γ рассекла сферу.

Величина малой оси эллипса зависит от угла α наклона секущей плоскости γ к горизонту, ее определяют по чертежу. Аналогично строят эллипс, который является профильной проекцией окружности сечения.

На рис. 8 шар пересекает сквозное отверстие прямоугольной формы, четыре плоскости которого перпендикулярны фронтальной плоскости проекций.

Каждая из четырех плоскостей прямоугольного отверстия пересекает сферу по окружностям, которые проецируются либо в отрезки прямых линий, либо в дуги окружностей.

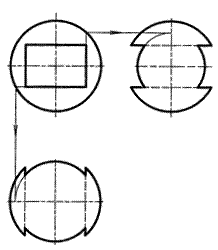
Рис. 8