Вопрос 7 – Метод кругло цилиндрических поверхностей скольжения

Основным недостатком рассмотренных выше методов является то, что полученные решения справедливы при относительно однородных пол физико-механическим свойствам массивах грунтов. В случае искусственно образованных откосов (откосы земляного полотна насыпей автомобильных дорог, плотин, дамб и т.п.) такая ситуация встречается достаточно часто. Однако при оценке устойчивости откосов глубоких выемок и природных склонов необходимо учитывать неоднородность грунтовых массивов. По инженерно-геологическим условиям потенциальные поверхности скольжения в массиве могут быть выраженными (прослои, оползневые смещения и т.д.) и не совпадать с предсказываемыми теорией предельного равновесия.

На практике чаще используют приближенные инженерные методы расчета.

К ним относят: метод кругло цилиндрических поверхностей скольжения, метод Шахунянца и др.

Метод кругло цилиндрических поверхностей скольжения впервые предложен К. Петерсоном в 1916 г. Метод называли «методом шведского геотехнического общества». В настоящее время имеются его различные модификации.

Потеря устойчивости откоса или склона, представленного на рисунке 26,а, может произойти в результате вращения отсека грунтового массива относительно некоторого центра О. Поверхность скольжения в этом случае будет представлена дугой окружности с радиусом r и центром в точке О. смещающийся массив рассматривают как недеформируемый (отвердевший) отсек, все точки которого участвуют в общем смещении. Коэффициент устойчивости определяют по формуле (7.19):

k _st = М_sr / М_sa , (7.19)

где М_sr и М_sa - моменты относительно центра вращения о всех сил, соответственно удерживающих и смещающих отсек.

Для определения входящих в формулу (7.19) моментов отсек грунтового массива разбивают вертикальными линиями на отдельные элементы. Характер разбивки назначают с учетом неоднородности грунта отсека и профиля склона так, чтобы в пределах основания каждого элемента прочностные характеристики φ и с были постоянными.

Вычисляют вертикальные силы, действующие на каждый элемент: собственный вес грунта в объеме элемента Р_giи равнодействующая нагрузки на его поверхности Р_qi. При необходимости могут быть учтены и другие воздействия (фильтрационные, сейсмические силы). Рассмотрим принципы их учета.

Равнодействующая сил Р_gi + Р_qi считается приложенной к основанию элемента и раскладывается на нормальную N_iи касательную T_iсоставляющие к участку дуги скольжения в точке их приложения.

Тогда:

N_i = (Р_gi + Р_qi) cos α_i ; T_i=(Р_gi + Р_qi) sin α_i ; (7.20)

Момент сил, вращающих отсек вокруг точки О, определится по выражению (7.21): n n

М_sa = r ∑ T_i = r ∑(Р_gi + Р_qi) sin α_i ; (7.21)

i=1 i=1

где n - число элементов в отсеке.

Принимают, что удерживающие силы T '_i в пределах основания каждого элемента обусловливаются сопротивлением сдвигу за счет внутреннего трения и сцепления грунта. Тогда с учетом выражения (5.2) можно записать (7.22):

T ' _i = N_i tg φ_i + c_i l_i = (Р_gi + Р_qi) cos α_i tg φ_i + c_i l_i , (7.22)

где l_i - длина дуги основания i-го элемента, определяемая по формуле:

l_i = b_i / cos α_i , (7.23)

b_i - ширина элемента.

Отсюда, выражение для определения момента сил, удерживающих отсек, будет иметь вид (7.24):

┌ n n ┐

М_sr = r │ ∑ (Р_gi + Р_qi) cos α_i tg φ_i + ∑ c_i l_i │ , (7.24)

└ i=1 i=1 ┘

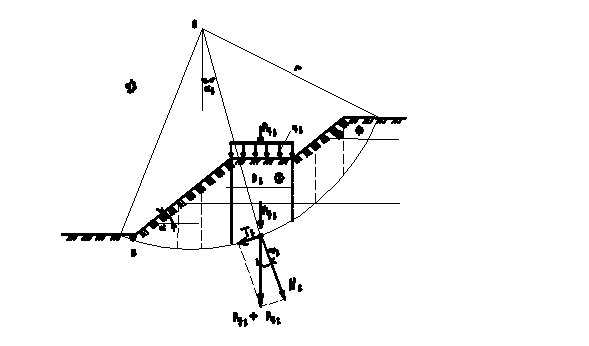
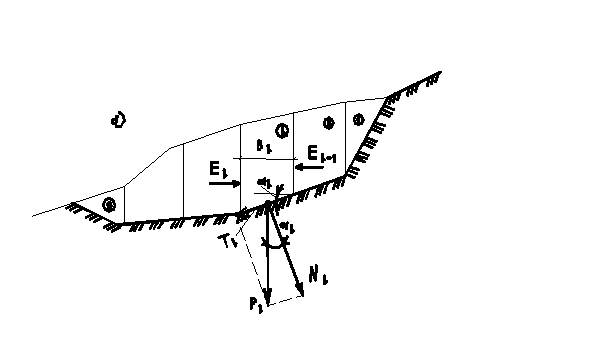
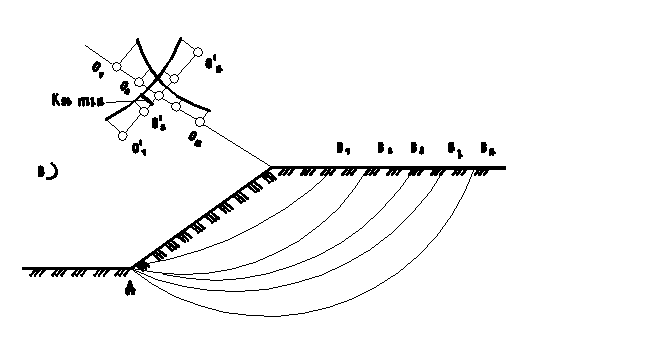
Рисунок 26 - Схема к расчету устойчивости откосов

методом кругло цилиндрических поверхностей скольжения:

1, 2, i … – номера элементов

Учитывая формулу (7.19), окончательно получим (7.25):

┌ n n ┐ / n

k _st =│ ∑ (Р_gi + Р_qi) cos α_i tg φ_i + ∑ c_i l_i │ / ∑ (Р_gi + Р_qi) sin α_i , (7.25)

└ i=1 i=1 ┘/ i=1

При k _st ≥ k ^н_st устойчивость отсека массива грунта относительно выбранного центра вращения О считается обеспеченной.

Сложность при практических расчетах заключается в том, что положение наиболее опасной поверхности скольжения неизвестно (неизвестно положение центра вращения и радиус дуги). Поэтому обычно проводится серия подобных расчетов при различных положениях центров вращения Ои значениях r. Чаще всего наиболее опасная поверхность скольжения проходит в районе нижней точки (подошвы) откоса или склона.

Один из приемов определения положения наиболее опасной поверхности скольжения заключается в следующем. Задаваясь координатами центров вращения О₁ , О ₂ , … , О _nна некоторой прямой положения центров вращения, определяют коэффициенты устойчивости k _{st , i} для соответствующих поверхностей скольжения и строят эпюру значений этих коэффициентов (Рисунок 26, в). Через точку О_min , соответствующую минимальному коэффициенту устойчивости, проводят по нормали второй отрезок и, располагая на нем новые центры вращенияО'₁ , О'₂ , … , О'_n , определяют коэффициенты устойчивости

k _{st , i} , для соответствующих поверхностей скольжения и строят эпюру этих коэффициентов (Рисунок 26, в). По этой эпюре вновь оценивают минимальное значение коэффициента устойчивости k _{st min}. Полученное значение k _{st min} и является мерой оценки устойчивости откоса или склона. Соответствующая этому значению коэффициента устойчивости кругло цилиндрическая поверхность скольжения рассматривается как наиболее опасная. Приведенная выше технология поиска наиболее опасной поверхности скольжения скорее соответствует технике «ручного» счета. В современных компьютерных программах при поиске наиболее вероятных поверхностей скольжения, как правило, назначается областьвозможных центров вращения с вариациями радиусов дуги скольжения. При k _{st min} ≥ k ^н_st устойчивость откоса и склона, согласно проектному заданию, считается обеспеченной.

Выполнение указанных расчетов «вручную» весьма трудоемко, поэтому разработаны многочисленные компьютерные программы с соответствующим сервисным обеспечением, позволяющие с минимальными затратами времени по вводу исходных данных получить обширную информацию об устойчивости откосов и склонов в количественных параметрах и графической интерпретации.