Наивероятнейшее число появлений события при повторных испытаниях по схеме Бернулли.

Опр. Наивероятнейшим числом появлений событияА в n независимыхиспытаниях называется такое натуральное число m₀, для которого вероятность, соответствующая этому числу, не менее вероятности каждого из остальных возможных чисел появления события А.

Должны выполняться следующие неравенства:

1) P_n(m₀)>=P_n(m₀+1)

2) P_n(m₀)>=P_n(m₀-1)

В силу формулы Бернулли

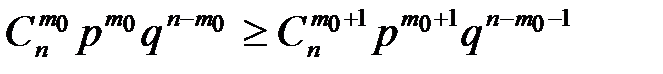
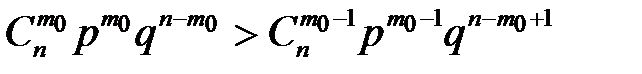
Решим неравенства относительно m₀

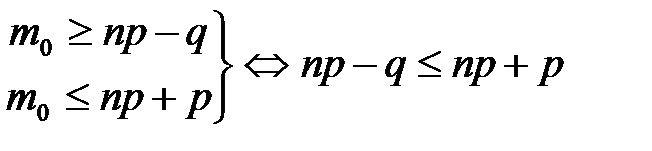
Длина интервала [np-q, np+p] равна –(np-q)+(np+p)=p+q=1.

Значит, может быть либо 2 значения m₀ (если (np-q) – целое число), либо 1 значение (если (np-q) – дробное число).