Корневой метод оценки устойчивости САУ

Устойчивость, очевидно, определяется свойствами САУ, т.е. ее характеристиками, в частности параметрами ее математической модели.

Известно, что для любого возмущения действующего на замкнутую САУ, справедливо:

y(t) = y_уст(t) + y_п(t) – решение дифференциальных уравнений САУ,

где y_уст(t) – частное решение неоднородного дифференциального уравнения с правой частью, описывающее вынужденный режим работы системы, который устанавливается по окончании переходного процесса.

y_п(t) – общее решение однородного уравнения.

W(s) + 1 = 0, т.е. характеристическое уравнение.

Здесь W(t) – передаточная функция разомкнутой САУ.

Т.е. 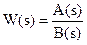, , 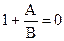D(s) = A(s) + B(s) = 0,

где D(s) – характеристический полином.

Решение y_п(t) затухает, т.е. стремится к нулю, если система устойчива, и наоборот y_п(t)→∞, если неустойчива.

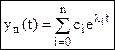, где λ_i – корни D(A) = 0

с_i – постоянные интегрирования, которые определяются начальными условиями.

В общем случае корни λ_i являются комплексными.

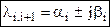где α_i – может быть как положительной, так и отрицательной величиной.

Каждая такая пара комплексно-сопряженных корней дает в выражении (1) составляющую переходного процесса вида

,

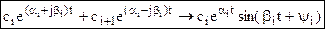где β_i – является круговой частотой, т.е. типа ω.

Доказательство:

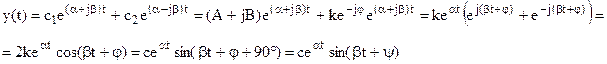
Здесь с₁ и с₂ также комплексно сопряжены

с₁ = А + jВ, с₂ = А – jВ

или

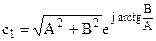
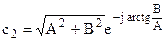
или , .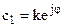

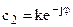Доказательство сопряженности с₁ и с₂:

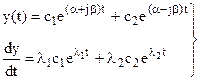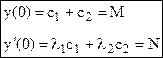→ , М, N, - начальные условия.

Отсюда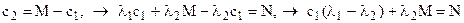

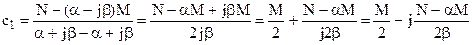
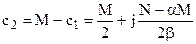, т.е. с₁ и с₂ – комплексно сопряжены.

При этом результат y(t) не зависит от знака перед β.

Например, пусть с₁ = А – jВ, с₂ = А + jВ, тогда

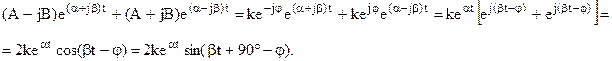
Анализ:

Как видно из этого соотношения переходный процесс затухает при α_i<0, и наоборот расходится при α_i>0.

При α_i=0 – корни мнимые, сто соответствует незатухающим колебаниям (граница устойчивости)

В частном случае при β_i=0 имеем действительные корни λ_i=α_i и соответственно апериодический переходный процесс.

Вывод: Условие устойчивости связано с условием α_i<0. Т.е. все корни D(s) (полюса знаменателя ПФ замкнутой САУ) должны иметь отрицательную действительную часть.

На комплексной плоскости условие устойчивости отображается в следующем виде:

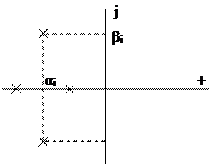Корни характеристического уравнения устойчивой системы располагаются в левой полуплоскости.

Наличие корня на мнимой оси означает, что система находится на границе устойчивости.

Проблема: Таким образом, если корни D(s) определены, то задача устойчивости можно сказать решена. В настоящее время корни полиномов легко определяются с помощью специальных программ, например, MathCad, MatLab.

Ранее ЭВМ не было и решение поставленной задачи представляло большие трудности. Поэтому все усилия были направлены на то, как определить устойчивость САУ, не решая дифференциальных уравнений. В результате были разработаны критерии устойчивости, которые позволяют оценивать устойчивость САУ по косвенным признакам.