УРАВНЕНИЕ ПУАЗЕЙЛЯ

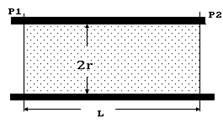
Уравнение Пуазейля описывает объемную скорость потока жидкости в зависимости от ее свойств, геометрических параметров сосуда и величины действующего давления. Пусть по некоторой цилиндрической трубе с радиусом r протекает жидкость с коэффициентом вязкости h (см. рис. 69).

Рассмотрим два сечения сосуда, удаленные на расстояние L. Если в первом сечении действует давление Р₁ , а во втором - Р₂ (для определенности Р₁ > Р₂), уравнение Пуазейля утверждает, что интенсивность потока жидкости, протекающей через сосуд будет

равна:

Q = (P₁ - P₂)R = P/R,

где R называется гидродинамическим сопротивлением. Его величина определяется следующим соотношением:

R = 8hL/ p r⁴

С учетом этого равенства интенсивность потока:

Q = (P₁ - P₂)p r⁴ /8 hL

Обращает внимание очень сильная зависимость объемной скорости от радиуса сосуда, по которому протекает жидкость. Поскольку радиус входит в четвертой степени, его уменьшение резко сокращает интенсивность потока.

Рис. 69