Момент силы относительно точки
В механике существует понятие о моменте силы относительно точки.
Моментом силы относительно точки называется взятое со знаком ( плюс или минус) произведение модуля силы на кратчайшее расстояние от точки до линии действия силы (рис. 12), т. е.
М0( 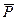 )= ±P h.
)= ±P h.
Точка О, относительно которой берется момент силы, называется центром момента; ОВ = h—кратчайшее расстояние от центра момента до линии действия силы — называется плечом силы относительно данной точки; знак плюс ставится в случае, если сила 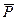 стремится повернуть плечо h против хода часовой стрелки, а знак минус — в противоположном направлении. Момент силы
стремится повернуть плечо h против хода часовой стрелки, а знак минус — в противоположном направлении. Момент силы 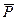 относительно точки О на рис. 12 положительный.
относительно точки О на рис. 12 положительный.
Из последнего равенства следует, что при h=0, т.е. когда О- центр моментов– расположен на линии действия силы 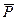 , М0(
, М0( 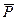 )=0. Как известно, сила—скользящий вектор, поэтому при переносе силы
)=0. Как известно, сила—скользящий вектор, поэтому при переносе силы  по линиям действия из точки А в любую другую точку A1, А2 и т. д. (рис. 12) длина плеча не изменится, а значит не изменится и значение момента силы относительно точки. Момент силы, как и момент пары, измеряют в ньютонометрах.
по линиям действия из точки А в любую другую точку A1, А2 и т. д. (рис. 12) длина плеча не изменится, а значит не изменится и значение момента силы относительно точки. Момент силы, как и момент пары, измеряют в ньютонометрах.
Рис.12. Момент силы  относительно точки O.
относительно точки O.
1.12. Уравнения равновесия плоской системы параллельных сил
Пусть к данному телу приложена система параллельных сил 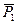 ,
, 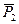 ,
, 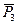 ,
, 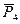 ,
,  (рис. 13). Через произвольную точку О, взятую в плоскости действия сил, проведем ось Ох, перпендикулярную силам, и ось Оу, параллельную этим силам. Запишем для данной системы сил уравнения равновесия
(рис. 13). Через произвольную точку О, взятую в плоскости действия сил, проведем ось Ох, перпендикулярную силам, и ось Оу, параллельную этим силам. Запишем для данной системы сил уравнения равновесия
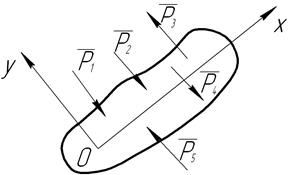
Рис.13. Система параллельных сил.


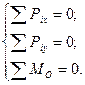
Каждая сила перпендикулярна оси Ох, и ее проекция на эту ось равна нулю. Следовательно, первое уравнение обращается в тождество 0 = 0 и выполняется независимо от того, уравновешиваются силы или нет. Таким образом, для плоской системы параллельных сил остается только два уравнения равновесия, причем на ось Оу силы проецируются в натуральную величину, так как эта ось параллельна заданным силам.
Система уравнений равновесия для плоской системы параллельных сил принимает вид
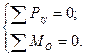
Уравнения равновесия для плоской системы параллельных сил можно записывать в виде
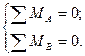
Точки А и В –произвольные точки , предпочтительно их взять на оси х, уравнение 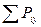 =0 служит для проверки правильности вычислений.
=0 служит для проверки правильности вычислений.
Итак, для произвольной плоской системы сил мы имеем три уравнения равновесия, а для плоской системы параллельных сил только два уравнения равновесия. Соответственно при решении задач на равновесие произвольной плоской системы сил можно найти три неизвестных, а при рассмотрении равновесия плоской системы параллельных сил — не более двух.
Если количество неизвестных превышает число уравнений статики, задача становится статически неопределимой.
1.13. Типы опор балок
В машинах и сооружениях очень часто встречаются тела удлиненной формы, называемые балками. Они в основном предназначены для восприятия поперечных нагрузок. Балки имеют специальные опорные устройства для сопряжения с другими элементами и передачи на них усилий. Опоры балок, рассматриваемых как плоские системы, бывают трех основных типов.
· Подвижная шарнирная опора (рис. 14, а). Такая опора не препятствует вращению конца балки и его перемещению вдоль плоскости качения. В ней может возникать только одна реакция, которая перпендикулярна плоскости качения и проходит через центр катка.
Схематическое изображение подвижной шарнирной опоры дано на рис. 14, б.
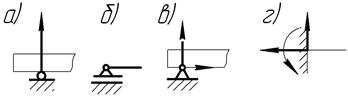
Рис. 14. Типы опор балок.
Подвижные опоры дают возможность балке беспрепятственно изменять свою длину при изменении температуры и тем самым устраняют возможность появления температурных напряжений.
· Неподвижная шарнирная опора (рис. 14, в). Такая опора допускает вращение конца балки, но устраняет поступательное перемещение ее в любом направлении Возникающую в ней реакцию можно разложить на две составляющие — горизонтальную и вертикальную
·Жесткая заделка, или защемление (рис. 14, г). Такое закрепление не допускает ни линейных, ни угловых перемещений опорного сечения. В этой опоре может в общем случае возникать реакция, которую обычно раскладывают на две составляющие (вертикальную и горизонтальную) и момент защемления (реактивный момент).
Балка с одним заделанным концом называется консольной балкойили просто консолью.
Если опорные реакции могут быть найдены из одних уравнений статики, то балки называют статически определимыми.Если же число неизвестных опорных реакций больше, чем число уравнений статики, возможных для данной задачи, то балки называют статически неопределимыми.
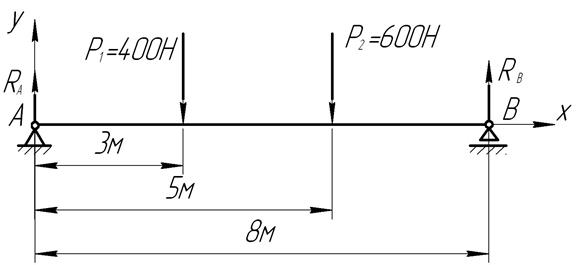
Пример.
Определить неизвестные параметры реакций опор А и В для заданной (рис.15 ) конструкции балки, нагруженной параллельными силами 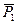 и
и 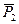 .
.
|
· Записываем уравнение равновесия балки как сумму моментов всех сил относительно опоры А.
Рис.15. Расчетная схема балки.
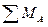 = RB*8 –P2*5 - P1*3 =0,
= RB*8 –P2*5 - P1*3 =0,
Откуда RB = 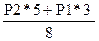 =
= 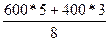 = 525Н.
= 525Н.
· Записываем уравнение равновесия балки как сумму моментов всех сил относительно опоры В.
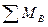 =-RA*8 +Р1*(8-3) +Р2*(8-5)=0,
=-RA*8 +Р1*(8-3) +Р2*(8-5)=0,
Откуда RA = 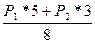 =
= 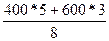 = 475Н.
= 475Н.
· Проверка правильности вычислений
Сумма проекций всех сил на ось Y должна равняться нулю.
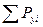 = RA –Р1 –Р2 + RB=475 -400-600+525 =0
= RA –Р1 –Р2 + RB=475 -400-600+525 =0
Дата добавления: 2015-06-17; просмотров: 2386;
