Признак и условие устойчивости замкнутых САУ.

Признаком устойчивости системы является следующее: если после воздействия на систему короткого импульса она с течением времени приходит в состояние покоя, то данная система устойчива. Математически это записывается так:

.

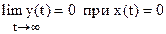Системы без обратных связей всегда устойчивы, в этих системах коэффициенты в (5.12) а_i = 0, i = 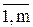, a₀ = 1.

Системы с обратными связями не всегда устойчивы. В неустойчивых системах возникают незатухающие колебания, которые нарушают нормальную работу систем и могут даже разрушить их.

САУ с передаточной функцией вида

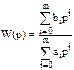
описывается дифференциальным уравнением

,

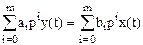где 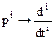символ дифференцирования.

После прекращения входного воздействия правая часть уравнения равна нулю, и оно превращается в однородное дифференциальное уравнение

.

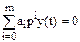Решение этого уравнения имеет следующий вид:

,

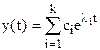где с_i - коэффициенты, 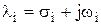- полюсы . Полюсы - это корни характеристического уравнения 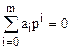, получаемого приравниванием нулю знаменателя функции W(р).

В общем случае при действительных коэффициентах а_i полюсы являются действительными или комплексно-сопряженными числами

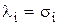или

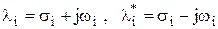
Тогда

.

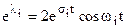Подставив это выражение в 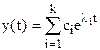, получим

.

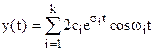Из этого выражения следует, что необходимым и достаточным условием устойчивости САУ, когда 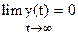, является условие 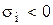, т.е. в устойчивых системах действительные части всех корней характеристического уравнения системы должны быть отрицательны.

Это простое на первый взгляд условие может быть проверено на практике только при степени характеристического уравнения 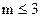. При 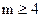общего аналитического решения характеристических уравнений не найдено. Поэтому при 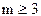для оценки устойчивости САУ предложено несколько косвенных методов проверки устойчивости САУ без решения характеристического уравнения.