Передаточные функции САУ при последовательном и параллельном соединении звеньев, с обратной связью.
1) Последовательное соединение звеньев
На рис.34 приведена схема последовательного или каскадного соединения звеньев с передаточными функциями Wi , i = 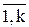 .
.
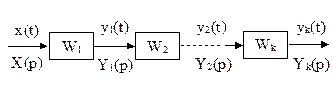
Рис.34 Схема последовательного соединения звеньев
Из схемы на рис.34 следует, что
Y1(p) = W1 X(p)
Y2(p) = W2 Y1(p
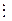
Yk(p) = Wk Yk-1(p)
По определению передаточная функция всей цепи
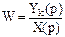
Y2(p) = W1 W2 X(p) , Yk(p) = W1 ×W2 ... Wk X(p).
W = W1 W2 ... Wk = 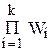
Из этого выражения следует, что при последовательном соединении звеньев результирующая передаточная функция равна произведению передаточных функций этих звеньев.
2) Параллельное соединение звеньев
На рис.35 приведена схема параллельного соединения звеньев с передаточными функциями Wi , i = 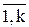 .
.
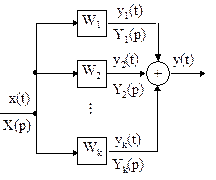
Рис.35 Схема параллельного соединения звеньев
Из рис.35 следует, что
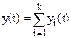 .
.
Тогда
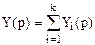 ,
,
причем
Yi(p) = Wi X(p).
По определению 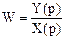 и с учетом
и с учетом 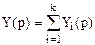 получим
получим
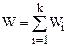
Из 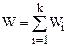 следует, что при параллельном соединении звеньев передаточная функция равна сумме передаточных функций этих звеньев.
следует, что при параллельном соединении звеньев передаточная функция равна сумме передаточных функций этих звеньев.
3) Соединение звеньев по схемам с обратными связями
Для улучшения качества работы САУ строятся по замкнутой схеме с обратной связью.
На рис.36 приведены две возможные схемы соединения звеньев с обратными связями.
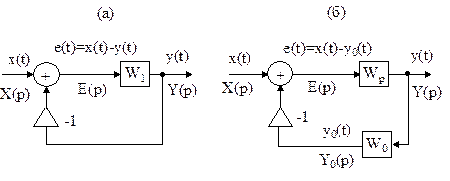
Рис.36 Две схемы соединения звеньев с обратными связями
Из схемы на рис.36а имеем
Y(p) = E(p) WР ,
где E(p) = X(p) - Y(p),
WР - передаточная функция при разомкнутой цепи обратной связи.
Тогда
Y(p) = X(p) WР - Y(p) WР,
откуда передаточная функция замкнутой системы на рис. 5.3а равна:
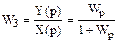
Из схемы на рис.36б имеем:
Y(p) = E(p) WР ,
где E(p) = X(p) - Y0 (p) = X(p) - Y(p) W0.
Тогда Y(p) = X(p) WР - Y(p) WР W0.
Откуда передаточная функция замкнутой системы на рис.36б равна
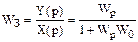
 .
.
Дата добавления: 2015-06-17; просмотров: 1568;
