Получение передаточных функций многоконтурных САУ.

На практике встречаются системы с двумя и более цепями обратной связи. Такие системы называются многоконтурными. На рис.37 приведена схема двухконтурной системы.

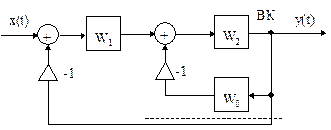
Рис.37 Схема двухконтурной системы

Передаточную функцию для этой системы получим поэтапно. Вначале получим выражение для передаточной функции внутреннего контура ВК, обведенного пунктиром. Схема ВК совпадает со схемой на рис.36б, для которой на основании 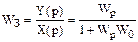получим:

.

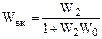Теперь схема совпадает с рис.36а, в котором W_Р = W₁ W_ВК .

Отсюда на основании 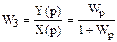получим

,

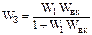где W_ВК определяется по приведенному выше выражению.

На рис.38а приведена схема трехконтурной системы, причем сигналы в цепи обратной связи берутся из разных точек схемы.

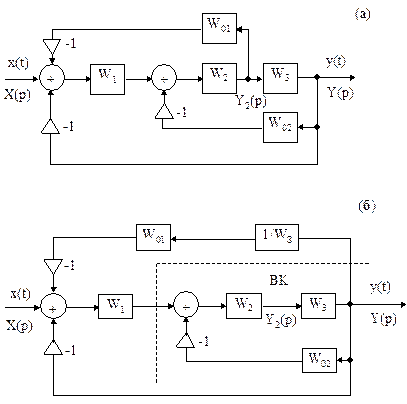
Рис.38 Две эквивалентные схемы трехконтурной системы

На рис.38б приведена эквивалентная ей вторая схема, в которой сигнал обратной связи берется из общей для всех трех цепей точки. Это удалось сделать благодаря тому, что дополнительно включили звено с передаточной функцией 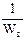. Покажем это. В схеме на рис.38а изображение сигнала на входе звена W₀₁ равно Y₂(p). Тогда Y(p) = Y₂(p) W₃ . Помножим Y(p) на 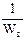и получим Y₂(p), то есть на звено W₀₁ поступает тот же самый сигнал, что и в схеме на рис.38а. Таким образом, эквивалентность схем на рис.38а и на рис.38б доказана.

Теперь поэтапно получим выражение для передаточной функции системы на рис.38б. Передаточная функция внутреннего контура на основании 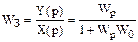с учетом 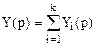равна

W_ВК = .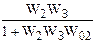

Так как две цепи обратных связей имеют общий входной сигнал y(t) и вводятся в одну точку на входе, следовательно они образуют звено передачи, соединенное по параллельной схеме. Передаточная функция этого звена равна 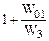. Тогда на основании 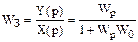получим выражение для передаточной функции системы на рис.38б:

W_З = ,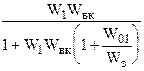

где W_ВК определяется по приведенному выше выражению.

Используя приведенные формулы, а также описанные приемы и преобразования, можно получить выражения для передаточных функций систем со сложной конфигурацией схемы и со многими цепями обратных связей.